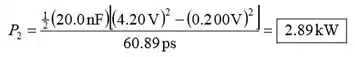Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 115
A figura 25-77 mostra a base do circuito de varrimento utilizado num osciloscópio. O interruptor S é um interruptor electrónico que fecha sempre que o potencial através do interruptor S aumenta para um valor Vc e abre quando o potencial através do interruptor S diminui para . O fem ε , que é muito maior que , carrega o condensador através de uma resistência . A resistência representa a resistência pequena mas finita do comutador electrónico. Num circuito típico, , , e . (a) Qual é a constante de tempo para o carregamento do condensador C? (b) Mostrar que à medida que o potencial através do interruptor S aumenta de para , o potencial através do condensador aumenta quase linearmente com o tempo. Dica: Usar a aproximação , para . (Esta aproximação de ex pode ser derivada usando a aproximação diferencial). (c) Qual deve ser alterado o valor de para que o condensador carregue de a em ? (d) Quanto tempo decorre durante a descarga do condensador quando o interruptor S fecha? (e) A que velocidade média é dissipada a energia na resistência durante a carga e na resistência do interruptor durante a descarga?
Passo 1
Eae galera! Belezinha? Vamos lá! Podemos utilizar a sua definição para encontrar a constante temporal do circuito de carga na Parte (a). Na Parte (b) podemos usar a expressão para a diferença potencial em função do tempo através de um condensador de carga e utilizar a dica dada na declaração do problema para mostrar que a tensão através do condensador aumenta quase linearmente ao longo do tempo necessário para levar o potencial através do comutador ao seu valor crítico. a) Quando o condensador está a carregar, o interruptor está aberto e a resistência no circuito de carga é R1. Por conseguinte, o circuito de carga é R1:
Passo 2
b) Expressaremos a tensão através do condensador de carga em função do tempo:
Utilizando a série de potências para a expansão de :
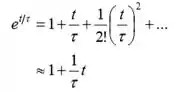
Substituindo para para obter:
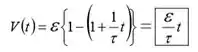
Passo 3
Utilizando o resultado obtido em (b), relacionar o tempo necessário para alterar a tensão através do condensador por um montante a :
Ou,
Substituindo numericamente:
Passo 4
No item d), Expressaremos a diferença potencial através do condensador como uma função do tempo:
Resolvendo para para obter:
Substituindo valores numéricos e achando ,
Passo 5
No item e), expressaremos o ritmo a que a energia é dissipada em R1 em função da sua resistência e da corrente através dela:
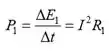
Como a corrente varia com o tempo, precisamos de nos integrar ao longo do tempo para encontrar :
Substituindo valores numéricos para achar ,
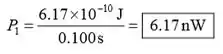
Para o ritmo a que a energia é dissipada na resistência do interruptor:
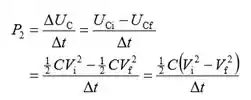
Substituir valores numéricos e avaliar :
