Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 64
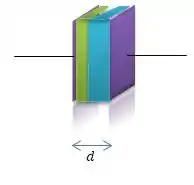
Um capacitor de placas paralelas tem placas separadas por uma distância . A capacitância deste capacitor é , quando não há dielétrico no espaçamento entre as placas. Entretanto, o espaçamento está completamente preenchido por dois dielétricos diferentes. Um dos dielétricos tem espessura e constante dielétrica , e o outro tem espessura e constante dielétrica . Determine a capacitância deste capacitor.
Passo 1
Cara... Imagina um capacitor de placas paralelas separados por uma distância e de capacitância quando a única coisa que tem dentro dele é vácuo (não tem dielétrico)...
O que queremos saber neste exercício é o que acontece com a capacitância deste capacitor quando inserimos nele dois dielétricos diferentes...
E aí? Nessa condição que acontece com a capacitância?
Passo 2
Cara, vamos filosofar um pouco sobre a capacitância em cima do capacitor sem nenhum material dielétrico no meio...
Agora, quando a gente insere dois materiais dielétricos (o verdim e o azul)...
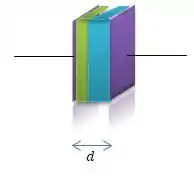
Repare que é como se tivéssemos criando dois capacitores em série...
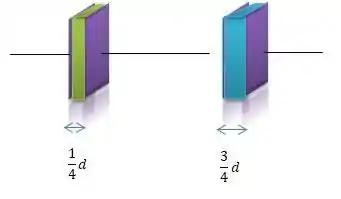
Percebe isso? Vou dizer que o capacitor da esquerda é o capacitor e o capacitor da direita é o capacitor . Então, o resultado da capacitância formado pela série entre eles pela nossa teoria será...
Agora, quem vem a ser cada capacitância?
Passo 3
Para o capacitor , como o material verdin tem constante dielétrica e as placas estão separadas por um distanciamento de ...
E, além disso, sabemos que é justamente esse carinha em negrito aí, então...
Passo 4
Para o capacitor , podemos fazer cálculos semelhantes...
Então, o valor da capacitância do capacitor com os dois materiais que estamos buscando...
Vai ser...
Então...