Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 65
Dois capacitores têm, ambos, duas placas condutoras com área de superfície e a espessura da camada de ar é igual a . Eles são conectados em paralelo, como mostra a Figura , e cada um tem carga na placa carregada positivamente. Uma lâmina que tem largura , área A e constante dielétrica , é inserida entre as placas de um dos capacitores. Calcule a nova carga na placa carregada positivamente deste capacitor depois que o equilíbrio eletrostático foi restabelecido.
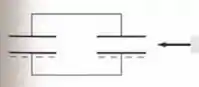
Passo 1
Beleza... Então vejamos primeiro o que está acontecendo, pode ser?
A gente tem aqui dois capacitores idênticos com carga conectados em paralelo...
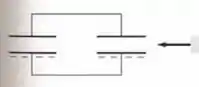
E aí de repente em um dos capacitores a gente insere um dielétrico nele...
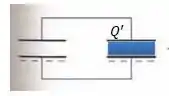
E ai as cargas vão se redistribuir pelo fato de que a capacitância de um deles vai mudar, de modo que vai sobrar em cima dele uma carga , que é justamente o que queremos encontrar neste problema, saca?
Mas para isso, tenha em mente que a carga total que é soma das cargas nas placas duas placas positivas dos capacitores sempre permanece constante...
Passo 2
Primeiro, vamos filosofar um pouco sobre os capacitores:
Antes de inserir o material dielétrico, no capacitor, a capacitância de cada capacitor ( e ) era...
A capacitância total, já que os capacitores estão em paralelo é...
Como de acordo com a teoria, dada que a tensão em cima dois capacitores é (antes de inserir o material...
Passo 3
Agora, vamos considerar que o dielétrico já foi inserido...
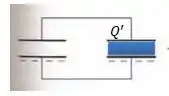
Nesse caso, a capacitância sofre uma alteração para...
Então a nova capacitância total será...
E pela como a carga total tem que se conservar...
Passo 4
Beleza! Agora é relativamente tranquilo, sabe por quê?
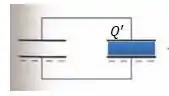
vai ser igual a...
Só que o novo , como vimos no passo anterior é...
Então...
Enquanto isso, é...
Agora olha que maneiro, quem era a carga antes do bagulho ser inserido?
Certo? Então...