Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 10
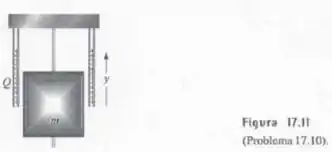
A Figura 17.11 mostra um corte em um capacitor cilíndrico carregado com carga . Os raios dos cilindros interno e externa são e , respectivamente. O cilindro interno, de massa , pode deslizar sem atrito em um eixo isolante, de forma que sua coordenada vertical é variável. Calcule o valor de para o qual o peso do cilindro interno é compensado pela força vertical elétrica que o outro cilindro faz sobre ele.
Passo 1
A primeira coisa que devemos lembrar é a capacitância de um capacitor cilindro de comprimento e raios interno e externo :
Nesse caso, o comprimento do capacitor será a distância que o cilindro interno penetra no cilindro externo, de modo que
Como a carga acumulada nas placas do capacitor é constante e igual a , podemos escrever a energia potencial do sistema por
Passo 2
A força que atua sobre o cilindro externo será então
Note que
Assim,
Mas note que
Logo,
Substituindo a expressão de :
Para que o cilindro seja sustentado, essa força deve se igualar ao peso do cilindro:
Daí,