Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.8 - Ex. 43

A Fig. 23-47 mostra uma seção reta de uma placa não condutora muito extensa com uma espessura d =   9,40   m m   e uma densidade volumétrica de cargas uniforme ρ   =   5,80   C / m 3

. A origem do eixo x está no centro da placa. Determine o módulo do campo elétrico (a) em x   = 0 ; (b) em x   =   2,00   m m ; (c) em x   =   4,70   m m ; (d) em x   =   26,0   m m .

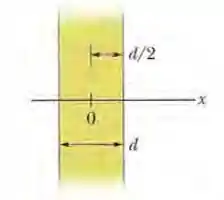
Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui deveremos encontrar o modulo do campo elétrico gerado por uma placa carregada. Para isso, iremos utilizar a Lei de Gauss.

Ao utilizar a Lei de Gauss, deveremos escolher sabiamente a superfície gaussiana.

Passo 2

Veja a superfície gaussiana pontilhada do desenho:

Pela Lei de Gauss:

∮ A E ⋅ d A = q i n t ϵ 0

Nesse caso, a carga interna a essa superfície é dada por (sendo o comprimento e a altura do paralelepípedo iguais a a ) :

q i n t = ρ ∙ V

= ρ ∙ a ⋅ 2 x ⋅ a

= ρ ∙ a 2 ∙ 2 x

Passo 3

Agora, o resultado da integral do campo elétrico ao longo da área gaussiana é o seguinte:

∮ A E ⋅ d A = E a ²

, pois nas faces superior e infeior o campo forma um ângulo de 90 º com o vetor normal à superfície, o que não ocorre com as superfícies laterais.

Daí, vem:

2 ϵ 0 E a ² = 2 a ² x ρ

E = ρ x ϵ 0

Onde ϵ 0 = p e r m i s s i v i d a d e   d o   v a c u o

Passo 4

Da expressão anterior podemos tirar resultados bem importantes:

  1. Para x = 0 , E = 0 ;
  2. Para x = 2,00   m m

    3. E = 5,8 ∙ 10 - 15 2,00 ∙ 10 - 3 8,85 ∙ 10 - 12 N C = 1,31   μ N / C

  3. Para x = 4,7   m m , substituindo os valores do enunciado e x na expressão anterior, temos que

    4. E = 5,8 ∙ 10 - 15 4,7 ∙ 10 - 3 8,85 ∙ 10 - 12 N C

    E = 3,08   μ N / C

    Passo 5

  4. Agora, se tivermos x = 26   m m , devemos usar uma superfície gaussiana parecida com a anterior, mas com as faces direita e esquerda ultrapassando a placa. Nesse caso, a carga envolvida vale q = a ² ⋅ d ⋅ ρ

Daí:

E = 5,8 ∙ 10 - 15 9.4 ∙ 10 - 3 2 8,85 ∙ 10 - 12 N C

= 3,08   μ N / C

Resposta

  1. 0
  2. 1,31 μ N C
  3. E = 3,08   μ N / C
  4. = 3,08   μ N / C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Modelo de Thomson para o átomo. Nos primeiros anos do século 20 , um dos modelos pioneiros para a estrutura foi proposto pelo físico inglês J. J. Thomson (o descobridor do elétron). Segundo o modelo d
Campo elétrico no interior de um átomo de hidrogênio. Um átomo de hidrogênio é constituído por um próton com carga + Q = 1,60 × 10 - 19C e um elétron com carga - Q = - 1,60 × 10 - 19C . Podemos consid
Uma região do espaço contém uma carga positiva Q que está distribuída uniformemente ao longo de uma esfera de tal modo que a densidade volumétrica de carga ρ r é dada por:Nessas relações, α é uma cons
Uma região do espaço contém uma carga positiva Q que está distribuída uniformemente ao longo de uma esfera de tal modo que a densidade volumétrica de carga ρ r é dada por:Nessas relações, α é uma cons
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado por E = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual