Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 65
Uma carga positiva será dividida em duas cargas puntiformes positivas, e . Mostre que, para uma dada separação , a força exercida por uma carga em outra é máxima se .
Passo 1
Nesse problema, vamos usar basicamente dois princípios:
- A conservação da carga elétrica; e
- Lei de Coulomb
A conservação da carga elétrica nos diz que a soma algébrica de carga, em um sistema isolado, deve permanecer sempre constante.
Já a lei de Coulomb nos diz que a força elétrica entre duas partículas carregadas é diretamente proporcional ao produto das cargas dessas partículas e inversamente proporcional ao quadrado da distância que separa as partículas.
Passo 2
Então, mãos à obra :D Se aplicarmos a conservação da carga elétrica, teremos que
E, pela lei de Coulomb, temos:
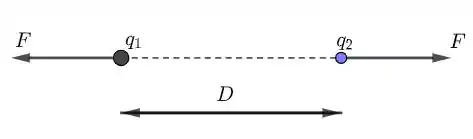
Assim, segue que
Passo 3
Assim, vamos supor que seja uma função de . Sendo assim, o máximo de ocorrerá quando . Assim,
ou seja,
Assim,
que é o que queríamos demonstrar!
Resposta
Ei, a resposta está no passo a passo :)