Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 64
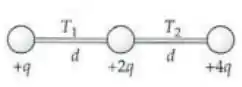
Uma carga puntiforme fixa de está conectada por cordas a cargas puntiformes e , como mostra a Figura 21-41. Determine as tensões e .
Passo 1
Vamos lá?! Inicialmente, notemos que todas as partículas carregadas fazem força uma sobre a outra. Lembre-se que para ocorrer o equilíbrio, a soma das forças sobre cada partícula deve ser igual a zero.
Passo 2
Como todo probleminha de forças, vamos tentar desenhar um diagrama para ajudar na visualização do problema. Veja:
Vemos que:
- Para o equilíbrio de :
- Para o equilíbrio de :
Passo 3
Vamos calcular cada uma dessas forças (em módulo). Faremos isso através da Lei de Coulomb. Note ainda que (ação reação). Logo,
Passo 4
Dessa forma, temos que
Resposta
Temos e .
Exercícios de Livros Relacionados
Um núcleo de ouro está a 100f m ( 1f m = 10 - 15m ) de um próton, que está inicialmente em repouso. Quando o próton é liberado, ele se afasta aceleradamente devido à repulsão gerada pela carga do núcl
Durante o experimento de Millikan usado para determinar a carga do elétron, uma microesfera de poliestireno carregada eletricamente é liberada em ar parado na presença de um campo elétrico vertical co
Durante um experimento famoso em 1919, Ernest Rutherford disparou núcleos de hélio duplamente ionizados (também conhecidos como partículas alfa) contra uma folha de ouro. Ele descobriu que virtualment
Uma partícula de massa m e carga q está confirnada a mover-se verticalmente dentro de um cilindro estreito sem atrito (Figura 21-47). No fundo do cilindro está uma carga puntiforme Q que tem o mesmo s
Um elétron (carga - e , massa m ) e um pósitron (carga + e , massa m ) giram em torno de seu centro de massa sob a influência da força coulombiana atrativa entre eles. Determine a rapidez v de cada pa