Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 69

Um bastão rígido de 1,00   m de comprimento está fixo por um ponto no seu centro (Figura 21-42) de forma que possa girar em torno dele. Uma carga q 1 = 5,00 × 10 - 7 C é colocada em uma extremidade do bastão, e uma carga q 2 = - q 1 é colocada a uma distância d = 10,0   c m diretamente baixo dela. (a) Qual é a força exercida por q 2 em q 1 ? (b) Qual é torque (medido em relação ao eixo de rotação) devido a esta força? (c) Para equilibrar a atração entre as duas cargas, penduramos um bloco a 25,0   c m do pivô, como mostrado. Que valor devemos escolher para a massa m do bloco? (d) Agora movemos o bloco e o penduramos a uma distância de 25,0   c m do ponto de fixo, no mesmo lado que estão as cargas. Mantendo q 1 e d os mesmos, que valor devemos escolher para q 2 para manter o sistema em equilíbrio, na horizontal?

Passo 1

Esse exercício cobra vários conteúdos misturados. Por isso, devemos rever alguns conceitos. Lembre-se que o torque de uma força F em torno de um ponto P é dado por:

τ = F d

onde d é a distância ortogonal da reta que contém a força até o ponto P (veja a figura abaixo)

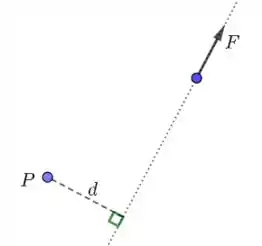
Vamos convencionar que, se a força estiver tendendo girar o sistema no sentido anti-horário, o torque será positivo; se estiver tendendo girar o sistema no sentido horário, será negativo. No caso acima, o torque tende a girar o sistema no sentido anti-horário. Logo, o torque será positivo.

Para que um corpo extenso esteja em equilíbrio rotacional, o somatório de todos os torques atuando sobre ele deve ser nulo.

Passo 2

  1. Para calcular a força elétrica, usamos a Lei de Coulomb:

    2. F = k q 1 q 2 d 2 = 9 × 10 9 5,00 × 10 - 7 5,00 × 10 - 7 2 0,1 2 = 0,225   N

    sendo que a força atua para baixo.

    Passo 3

  2. Veja a figura:

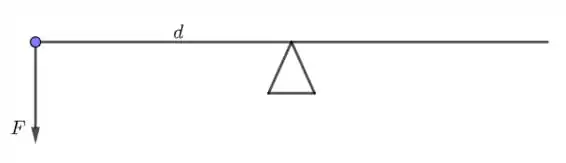
    3. Note que d = l 2 , onde l = 1,00   m é o comprimento da barra.

    Assim,

    τ = F d = 0,225 0,50 = 0,112   N ⋅ m

    Se a gente fosse colocar os sinais, colocaríamos τ = + 0,112   N ⋅ m , pois a força elétrica tende a girar a barra no sentido anti-horário.

    Passo 4

  3. Para que a barra fique em equilíbrio, o torque total sobre a barra deve ser nulo.

    4. O torque do peso deve ser:

    τ = - m g × 0,25

    Veja que é negativo pois tende a girar a barra no sentido horário. Dessa forma,

    τ t o t a l = 0 ⟹ 0,112 - m g × 0,25 = 0 m = 0,112 0,25 g = 0,112 0,25 × 9,8 = 45,8 × 10 - 3   k g

    ou seja, m = 45,8   g .

    Passo 5

  4. Note que o módulo do torque peso continuaria sendo igual. Porém, agora ele seria positivo. Assim, a força elétrica precisaria mudar de sentido (ou seja, ser uma força repulsiva).

F . Sendo assim, a carga deveria apenas mudar de sinal (para que fosse repulsiva). Portanto, q 2 = - 5,00 × 10 - 7   C

Resposta

  1. 0,225   N
  2. 0,112   N ⋅ m
  3. 45,8   g
  4. - 5,00 × 10 - 7   C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas moléculas neutras no eixo x atraem-se mutuamente. Cada molécula tem um monte de dipolo p → , e estes momentos de dipolo estão na direção + x e estão separados por uma distância d . Deduza uma exp
No problema 86 está uma descrição do experimento de Millikan usado para determinar a carga do elétron. Durante o experimento, uma chave é usada para inverter o sentido do campo elétrico sem alterar se
Duas esferas condutoras iguais, mantidas fixas, se atraem mutuamente com uma força eletrostática de 0,108N quando a distância entre os centros é 50,0c m . As esferas são ligadas por um fio condutor de
Neurônios são componentes do sistema nervoso do corpo que transmitem sinais à medida que impulsos elétricos se propagam ao longo de sua extensão. Essa propagação acontece quando cargas subitamente ent
Uma partícula possui carga igual a - 5,00n C . (a) Determine o módulo, a direção e o sentido do campo elétrico produzido por essa partícula em um ponto situado a 0,250m diretamente acima dela. (b) A q