Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 32

Uma carga puntiforme +3e está na origem e uma segunda carga puntiforme -2e está no eixo x em x = a. (a) Represente a função potencial V(x) versus x para todos os pontos no eixo x. (b) Em que ponto ou pontos, se existir algum, V = 0 no eixo x?(c) Em que ponto ou pontos, se existir algum no eixo x, o campo elétrico é zero? Estas posições são as mesmas encontradas na Parte (b)? Explique sua resposta. (d) Quanto trabalho é necessário para trazer uma terceira carga +e até o ponto x = 1/2 a no eixo x?

Passo 1

A figura abaixo representa o enunciado.

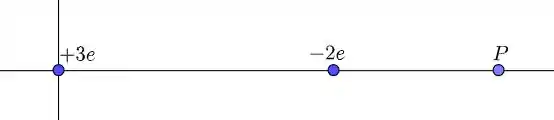
  1. Suponha que o ponto P está no ponto x . Assim, temos que

    2. V = k + 3 e d 1 + k - 2 e d 2

    onde

    d 1 = x

    e

    d 2 = x - a

    Dessa forma, temos que

    V = 3 k e x - 2 k e x - a

    Passo 2

  2. Devemos resolver a equação

    3. 3 k q x - 2 k q x - a = 0 3 k q x = 2 k q x - a 3 x = 2 x - a 3 x - a = 2 x

    Para resolver essa equação, devemos tomar alguns intervalos:

  • Se x < 0 , temos x - a = - x + a e x = - x . Dessa forma, temos

    • 3 - x + a = - 2 x - 3 x + 3 a = - 2 x x = 3 a

  • Se 0 < x < a , temos x - a = - x + a , x = x . Dessa forma,

    • 3 - x + a = 2 x 3 a = 5 x ⟹ x = 3 a 5

  • Se x > a , temos x - a = x - a e x = x . Dessa forma,

3 x - a = 2 x x = 3 a

Passo 2

  • Notemos que o campo elétrico só pode ser zero para x > a ou x < 0 , pois em 0 < x < a o campo da carga negativa fortalece o campo da carga negativa. Para qualquer uma dessa duas posições, podemos escrever

    • E x = k 3 e x 2 + k - 2 e x - a 2

    Fazendo E x = 0 , temos

    3 k e x 2 = 2 k e x - a 2 3 x - a 2 = 2 x 2 x 2 - 6 a x + 3 a 2 = 0

    Resolvendo, por Bhaskara, encontramos

    x = 5,4 a     o u   x = 0,55 a

    Porém, a segunda raiz não é válida, pois ela está no intervalo 0 < x < a . Assim, o campo elétrico é nulo apenas em x = 5,4 a . Repare que o campo elétrico não é zero nos mesmos pontos em que o potencial é zero. Isso geralmente acontece, e não é muito comum que as duas grandezas se anulem no mesmo ponto.

    Passo 3

  • Inicialmente, vamos calcular o potencial em x = 1 2 a :

    • V a = 3 k e 0,5 a - 2 k e 0,5 a - a = 6 k e a - 4 k e a V a = 2 k e a

    No infinito, temos V ∞ = 0 . Logo,

    W = e ⋅ V a - V ∞ = e ⋅ 2 k e a W = 2 k e 2 a

    Resposta

    1. V = = 3 k e x - 2 k e x - a
    2. x = 3 5 a ou x = 3 a ;
    3. x = 5,4 a .
    4. W = 2 k e 2 a
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Considere que duas partículas puntiformes, com carga + e , estão em repouso e separadas por 1,50 × 10 - 13m . (a) Quanto trabalho foi necessário para coloca-las juntas a partir de uma separação muito
    Cargas puntiformes q 1 ,q 2 , q 3 estão fixas nos vértices de um triângulo equilátero cujos lados tem comprimento de 2,50m . Determine a energia potencial eletrostática deste sistema de cargas para os
    Um condutor esférico de raio R 1 está carregado com 20k V . Quando ele é conectado através de um fio condutor muito fino e longo, a um segundo condutor esférico bem distante, seu potencial cai para 12
    Uma carga puntiforme positiva igual a 4,80 × 10 - 19C está separada de uma carga puntiforme negativa de mesma magnitude por 6,40 × 10 - 10m . Qual é o potencial elétrico em um ponto a 9,20 × 10 - 10m
    Duas cargas puntiformes positivas com carga + q estão no eixo y em y = + a e y = - a . Determine o potencial elétrico em qualquer ponto do eixo x . (b) Use seu resultado na parte (a) para determinar o