Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 39

Três cargas puntiformes idênticas, cada uma com uma carga igual a q , estão no plano x y . Duas das cargas estão no eixo y em y = - a e y = + a , e a terceira carga está no eixo x em x = a . (a) Determine o potencial como uma função da posição ao longo do eixo x . (b) Use o resultado da parte (a) para obter uma expressão para E x x , a componente x do campo elétrico como uma função de x . Confira suas respostas para as partes (a) e (b) na origem e quando x tende a ∞ para ver se elas fornecem os resultados esperados.

Passo 1

Fala ai galera, beleza? A figura a seguir representa a configuração de cargas dita no enunciado:

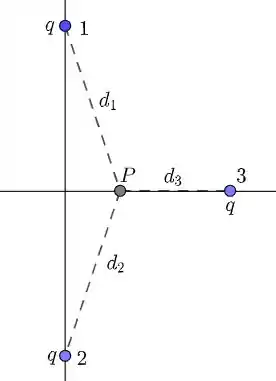
Seja P um ponto na posição x . Queremos calcular o potencial elétrico em P para qualquer valor de x !

Passo 2

  1. Temos que

    2. V = V 1 + V 2 + V 3

    Onde V 1 é o potencial devido a carga 1 , V 2 é o potencial devido a carga 2 e V 3 é o potencial devido a carga 3 . Notemos que d 1 = d 2 = a 2 + x 2 . Dessa forma, temos

    V 1 = V 2 = k q a 2 + x 2

    Além disso,

    V 3 = k q d 3 = k q x - a

    Assim, temos que

    V = 2 k q a 2 + x 2 + k q x - a

    Veja que tal fórmula faz sentido apenas para x ≠ a !

    Passo 3

  2. Para x < a , temos que

V = k q 2 a 2 + x 2 - 1 x - a

pois x - a = - x - a . Assim,

E x = - d V d x = - k q - 2 x a 2 + x 2 3 / 2 + 1 x - a 2 E x = 2 k q a 2 + x 2 3 / 2 - k q x - a 2

Para x > a , temos que

V = k q 2 a 2 + x 2 + 1 x - a

De forma que

E x = - d V d x = - k q - 2 x a 2 + x 2 3 / 2 - 1 x - a 2

Logo,

E x = 2 k q x a 2 + x 2 3 / 2 + k q x - a 2

Passo 3

  • Para x = 0 , temos

    • V 0 = k q 2 a - 1 a = k q a

    E 0 = 2 k q a 2 - k q a 2 = k q a 2

  • Para x → ∞ , temos

V ∞ = 0 E ∞ = 0

que é exatamente o que esperávamos!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O potencial elétrico ao longo do eixo x é dado por V = 50 x - 100 x V , onde x está em metros. Qual é o campo correspondente Ex em (a) x = 1,0 m e em (b) x = 2,0 m ?
O gerador de Van de Graaf é um dispositivo para geração de um grande potencial elétrico através da acumulação de carga sobre uma esfera oca metálica. Um típico modelo para demonstrações em sala de aul
Uma casca esférica fina de raio R possui uma carga total Q. Qual é o potencial elétrico no centro da casca?
a. Encontre uma expressão algébrica em função do potencial V 0 e do raio R da esfera para a intensidade E → 0 do campo elétrico na superfície de uma esfera carregada.b. Qual é a intensidade de campo e
Na Fig. 26-2 o campo elétrico E é maior do lado esquerdo ou do lado direito da figura?