Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Exercício - Ex. 10

Uma carga puntiforme q 1 = 4,0   n C está localizada sobre o eixo O x , no ponto x = 2,0   m , e uma segunda carga puntiforme q 2 = - 6,0   n C está localizada sobre o eixo O y , no ponto y = 1,0   m . Qual é o fluxo elétrico total produzido por essas cargas através de uma superfície esférica centralizada na origem e com um raio de a   0,50   m ? b   1,50   m ? c   2,50   m ?

Passo 1

Inicialmente, para determinar o fluxo elétrico para cada raio, a superfície esférica de cada caso é considerada como a própria superfície gaussiana.

Assim, o fluxo irá depender da existência de pelo menos uma carga no interior dessa superfície esférica gaussiana.

Passo 2

Para o primeiro caso, o esboço pode ser:

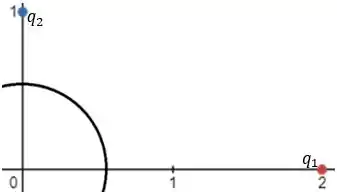
Como nenhuma das cargas está contida dentro da superfície esférica, então não há geração de fluxo por elas. Logo:

Φ a = 0

Passo 3

Agora, para o segundo caso temos:

Nessa situação, é visível que a carga q 2 está dentro da superfície e, portanto, o seu fluxo elétrico será dado por:

Φ b = E A = q ϵ 0 → Φ b = - 6 × 10 - 9   C 8,854 × 10 - 12   C 2 / N m 2 → Φ b = - 677,66   N m 2 C

Passo 4

Para a última situação, é nítido que a superfície esférica envolverá ambas as cargas pelo fato do seu raio ser maior do que as coordenadas de cada uma delas. Então, o fluxo total será a soma dos fluxos gerado por cada carga, ou seja:

Φ c = E A = q ϵ 0 → Φ c = 4 - 6 × 10 - 9   C 8,854 × 10 - 12   C 2 / N m 2 → Φ c = - 225,89   N m 2 C

Resposta

a   0

b - 677,66   N m 2 C

c   - 225,89   N m 2 C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera sólida não condutora de raio R tem uma densidade volumétrica de arga que é proporcional à distância ao centro. Ou seja, ρ = A r para r ≤ R , onde A é uma constante. (a) Determine a carga to
Mostre que o campo elétrico devido a uma fina casca cilíndrica, infinitamente longa e uniformemente carregada, com raio a e densidade superficial de carga σ , é dado pelas seguintes expressões: E = 0
Uma esfera sólida não condutora de raio 1,00c m tem uma densidade volumétrica uniforme de carga. A magnitude do campo elétrico a 2,00c m do centro da esfera é 1,88 × 10 3N / C . (a) Qual é a densidade
Uma esfera de raio R em densidade volumétrica de carga ρ = C / r 2 para rR onde C é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões para o campo elét
Um cilindro sólido não condutor infinitamente longo, de raio a , tem densidade volumétrica de carga não uniforme. Esta densidade varia linearmente com a distância R , a distância perpendicular ao seu