Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Exercício - Ex. 2
Uma placa plana possui a forma de um retângulo com lados de e . A placa está imersa em um campo elétrico uniforme com módulo igual a e cuja direção forma um ângulo de com o plano da placa (Figura ). Calcule o módulo do fluxo elétrico total através da placa.
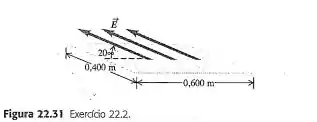
Passo 1
Visto que as variáveis para o cálculo do fluxo elétrico são dadas como constantes, a equação para isso é:
No entanto, o ângulo dado não é o da equação, visto que não está entre o vetor normal à superfície e o sentido do campo elétrico e, sim, é o complementar do ângulo desejado. Logo:
Passo 2
Logo, substituindo na equação:
Resposta
Exercícios de Livros Relacionados
Dois discos de raio igual a 10c m está separados pela distância de 1,0m m e com seus eixos de simetria coincidentes. Um disco tem densidade de carga uniforme σ = 3,0 ⋅ 10 - 10C / c m 2 e outro tem den
Uma esfera de raio R tem uma carga q uniformemente distribuída em seu volume. Utilize a lei de Gauss e considerações de simetria para calcular o campo elétrico à distância r do centra da esfera, (a) p
A Terra está negativamente carregada em relação à alta atmosfera, de forma que na proximidade do solo existe um campo elétrico médio de 100N / C , apontando para baixo. Qual é a carga total da Terra?
A Figura 15.18 mostra dois planos infinitos paralelos, contendo densidades uniformes de carga de mesmo módulo σ e sinais contrários.a) Calcule o campo criado pelo sistema.b) Esboce as linhas de força
A Figura 15.20 mostra um balde e uma partícula com carga q situada no plano da sua face aberta. Calcule o fluxo do campo elétrico na superfície do balde.