Uma partícula puntiforme que tem carga e massa desconhecida, , é liberada a partir do repouso em uma região que tem campo elétrico uniforme dirigido verticalmente para baixo. A partícula atinge o solo com uma rapidez , onde é a altitude inicial da partícula. Determine em termos de e .
Passo 1
Esse problema nos lembra muito a queda livre, assunto estudado em Física I (cinemática). Aqui, a situação é praticamente a mesma, mas em vez de termos apenas um campo gravitacional, temos também um campo elétrico. Veja:
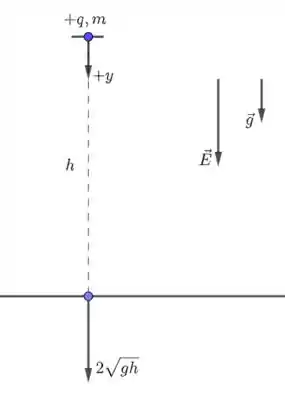
Na figura, adotamos um eixo orientado verticalmente para baixo, com na posição inicial da partícula.
Passo 2
Como a partícula possui carga positiva e o campo elétrico está orientado para baixo, segue que a partícula sofrerá uma força elétrica também para baixo. Não podemos nos esquecer do peso :D. Logo, a força total sobre a partícula será:
Pela 2ª Lei de Newton,
Passo 3
Note que a aceleração é constante. Dessa forma, por Torricelli, temos:
Passo 4
Outra resolução seria por trabalho energia. Note que a força elétrica é constante. Sendo assim, o trabalho dela vale . Da mesma forma, temos para a força peso, . Logo, pelo teorema da energia cinética,
onde
pois a partícula começa do repouso, e
Dessa forma,
Resposta
A massa vale .