Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 62
Cargas puntiformes de , e estão localizadas no eixo em , e , respectivamente. Calcule o campo elétrico no eixo em e em . Há pontos onde o módulo do campo elétrico é igual a zero? Se a resposta for positiva, onde estão estes pontos?
Passo 1
Nesse problema, queremos calcular o campo elétrico em diversos pontos. Como temos cargas elétricas pontuais, poderemos usar a fórmula:
Essa equação nos dá o campo elétrico de apenas uma partícula. Para várias partículas, devemos usar o princípio da superposição, que diz que o campo resultante será a soma vetorial de cada campo elétrico.
Passo 2
Vamos calcular o campo elétrico para um ponto qualquer que esteja à direita de , pois assim poderemos calcular o campo em e em de maneira mais rápida.
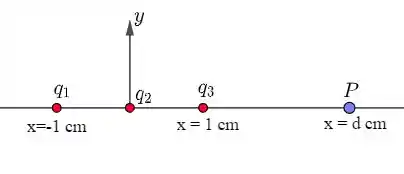
O campo resultante em é:
Passo 3
Assim, conseguimos encontrar uma função que nos dá quando conhecemos .
- Para calcular o campo em , teremos:
- Para calcular o campo em , teremos:
Como , significa que o campo das cargas positivas é maior do que da negativa. Sendo assim, o campo em é de afastamento, de modo que
Como , vemos que o campo das cargas positivas é maior do que da negativa. Sendo assim, o campo em é de afastamento. Logo,
Passo 4
Agora, para analisarmos se há pontos em que o campo elétrico é nulo, deveremos tomar cuidado. Vamos dividir em quatro regiões. Veja:
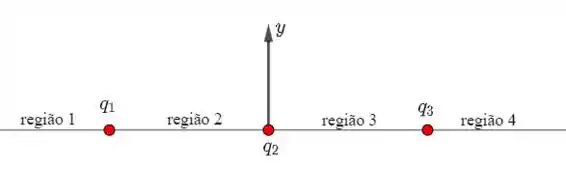
Vamos calcular o campo elétrico para cada uma das regiões:
- Região 1
- Região 2
- Região 3
- Região 4
Para que , temos que
Essa equação é bem complicadinha de se resolver analiticamente... usando uma calculadora, descobrimos que
Notemos que todas as cargas geram campo elétrico para a esquerda na região 2. Assim, não temos nenhum ponto da região 2 em que o campo elétrico é nulo.
Temos que
Assim, para que o campo elétrico seja nulo, basta analisar a equação
Novamente, essa equação é bem complicada de ser resolvida analiticamente. Usando uma calculadora, temos que
Na região 4, o campo elétrico com certeza nunca se anula. Note que e fazem campo para a direita, enquanto faz campo para a esquerda (na região 4). Porém, e a distância entre os pontos da região e é menor do que a distância até a carga . Logo, o campo sempre apontará para a direita...
Resposta
- e
- e .