Carlos está pedalando, aproximando-se de um riacho de 7,0 m de largura. Uma rampa inclinada de 10° foi construída para aqueles corajosos que queiram tentar atravessar o riacho. Carlos desenvolve a máxima rapidez da bicicleta, 40 km/h. (a) Carlos deve tentar o salto ou frear? (b) Qual a menor rapidez que uma bicicleta deve ter, para realizar o salto? Suponha as margens do riacho no mesmo nível (Ignore a resistência do ar.)

Oi galera, tudo bem? É muito importante tentar visualizar direitinho toda a situação apresentada no problema. Pra te ajudar trouxe aqui um desenho que esquematiza tudo certinho.

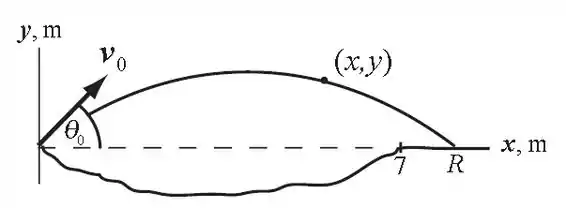
A problemática da questão é a seguinte... Carlos vai conseguir chegar na outra margem ou não? Para saber isso é só fazer os cálculos.

Carlos está a uma velocidade inicial de 40 km/h . Sempre é bom deixar as medidas nas mesmas grandezas, então vamos transformar essa velocidade para m/s. Para isso é só dividir por 3,6:

Agora vamos ver quais equações podemos usar pra resolver nosso problema.

O movimento da horizontal (em x) não possui aceleração, ou seja, ela é zero. Então o movimento é uniforme. Por isso para resolver o problema usaremos:

Onde

Na vertical, como a aceleração é a gravidade, o movimento é acelerado. Por isso podemos usar as equações:

Onde

Para verificar se é possível precisamos do tempo do movimento. Podemos achar o tempo de subida com os dados disponibilizados.

Resolvendo temos que: . O tempo do movimento é o dobro do tempo de subida, portanto:

Agora é só substituir na equação do espaço horizontal para saber o alcance.

Isso quer dizer que, para as condições dadas, Carlos não conseguiria chegar até a outra margem.