Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.Problemas Adicionais - Ex. 125

125- Uma bala é disparada por um canhão ao nível do mar com uma velocidade inicial de 82 m/s e um ângulo inicial de 45° e atinge uma distância horizontal de 686 m. Qual seria o aumento da distância atingida pela bala se o canhão estivesse a 30 m de altura?

Passo 1

Dados da questão:

y = 0 ; θ 0 = 45 ;     v 0 = 82 m s ;     R = 686   m

A questão quer saber o R para caso y = 30 e a diferença da dos dados de cima.

Passo 2

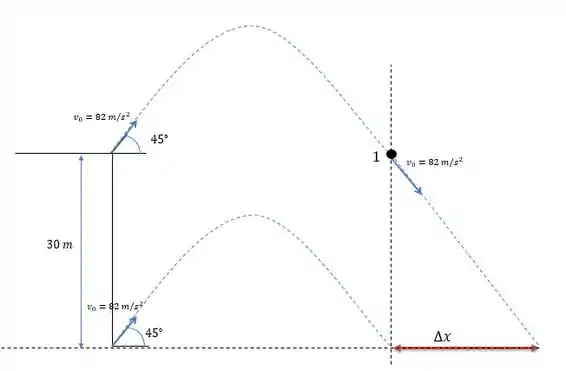
Primeiro vamos calcular a componente horizontal da bala.

v 0 x = v 0 cos ⁡ θ = 82 × cos ⁡ 45 = 57.98   m / s

Agora o tempo total de percurso do projétil em y = 0 .

v x = R t

t = R v x = 686 57.98 = 686 57.98 = 11.83   s

O projétil em y 0 = 30   m percorre a mesma distância no mesmo tempo, porém quando ela volta em R = 686   m o vetor v 0 volta com sentido contrário ao do inicial (no ponto 1).

Passo 3

Logo o tempo total percorrido pela partícula que começa em cima será:

Δ y = v 0 y t - 1 2 g t 2

0 - 30 = ( 82 sin ⁡ 45 ) t - 9.81 2 t 2

- 4.905 t 2 + 57.99 t + 30 = 0

Por Bhaskara encontramos os valores de t iguais a:

t 1 ; t 2 = ( - 0.496 ; 12.32 )

Onde pegaremos somente os valores positivos de t .

t = 12.32   s

Passo 4

Logo a distância Δ x será o valor da componente horizontal da velocidade multiplicado pela diferença dos tempos entre os dois projéteis.

Δ x = 57.98 × 12.32 - 11.83 = 28.41   m

Resposta

Δ x = 28.41   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41. a . Um projétil é lançado com velocidade v 0 e ângulo θ . Derive uma expressão para a altura máxima h atingida pelo projétil. b . Uma bola de beisebol é arremessada com 33,6m / s de velocidade. Ca
39. Uma partícula parte do repouso em r 0 → = 9,0j ^m e move-se no plano x y com a velocidade representada na FIGURA P4.39. A partícula passa por dentro de uma argola de arame localizada em r 1 → = 20
10 . | Um estudante de física no planeta Exidor arremessa uma bola, e ela segue a trajetória parabólica mostrada na F I G U R AE X 4.10 . A posição da bola é mostrada em intervalos de 1 s até t=3 s .
13 . | Um avião de suprimentos precisa soltar um pacote de alimentos para cientistas que estão trabalhando em um glaciar na Groenlândia. O avião voa a 100m de altura do glaciar com uma velocidade de 1
14 . | Um marinheiro sobe ao topo do mastro, 15 m acima do convés, para procurar por terra enquanto o navio se move constantemente a 4,0m / s em águas calmas. Infelizmente, ele deixa cair sua luneta n