Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 71

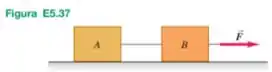
Duas caixas estão ligadas por uma corda sobre uma superfície horizontal (Figura E5.37). O coeficiente de atrito cinético entre cada caixa e a superfície é μ C = 0,30 . A caixa B tem massa de 5,00   k g e a caixa A tem massa m . Uma força F com módulo 40,0   N e direção 53,1 ° acima da horizontal é aplicada à caixa de 5,00   k g , e as duas se movem para direita com a = 1,50   m / s 2 . (a) Qual é a tensão na corda que conecta as caixas? (b) Qual é o valor de m ?

Passo 1

Fala pessoal, bora resolver um probleminha de dinâmica?

O primeiro passo é desenhar todas as forças que agem em cada caixa:

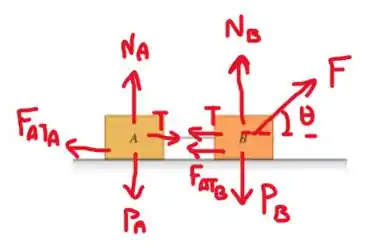
Na caixa B, temos a força F , o peso, a normal, o atrito e a tração. Já na caixa A nós temos a normal, peso, tração e atrito.

Como as caixas não se movimento na vertical, as forças verticais em cada uma devem se anular:

N A = P A N B + F y = P B → N A = m A   g N B + F   s e n   θ = m B   g

Desta forma, achamos relações para N A e N B :

N A = m A   g                 e               N B = m B   g - F   s e n   θ

Passo 2

O próximo passo é considerar o movimento na direção horizontal escrevendo a segunda lei de Newton para cada caixa:

F x - T - F a t B = m B   a T - F a t A = m A   a

Assim,

F cos ⁡ θ - T - μ C N B = m B   a T - μ C N A = m A   a

Usando as expressões para N A e N B achadas no passo 1:

F cos ⁡ θ - T - μ C m B   g - F   s e n   θ = m B   a T - μ C m A   g = m A   a

Somando as equações, nós achamos

F cos ⁡ θ - μ c m B g - μ C m A g + μ C F   s e n   θ = m B a + m A a

Vamos isolar m A :

a + μ C g m A = F cos ⁡ θ - μ C m B g + μ C F   s e n   θ - m B a

Logo,

m A = F cos ⁡ θ + μ C   s e n   θ - m B a + μ C g a + μ C g

Ou ainda,

m A = F cos ⁡ θ + μ C   s e n   θ a + μ C g - m B

Substituindo os valores:

m A = 40,0 ⋅ cos ⁡ 53,1 ° - 0,30 ⋅ s e n   53,1 ° 1,50 + 0,30 ⋅ 9,8 - 5,00

Com isso, achamos

m A = 2,57   k g

Passo 3

Para encontrar a tração, substituímos na equação:

T - μ C m A g = m A a → T = m A a + μ C g

Logo,

T = 2,57 ⋅ ( 1,50 + 0,30 ⋅ 9,8 )

Portanto,

T = 11,4   N

Resposta

m A = 2,57   k g

T = 11,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 6-51, um caixote escorrega para baixo em uma vala inclinada cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é μ k . Qual é a aceleração do caixote e
Na Fig. 6-59, o bloco 1 de massa m 1=2,0k g e o bloco 2 de massa m 2=1,0k g estão ligados por um fio de massa desprezível. O bloco 2 é empurrado por uma força F de módulo 20N que faz um ângulo θ=35 °
O bloco A da Fig. 6-56 possui massa m a=4,0k g e o bloco B possui massa m b=2,0k g . O coeficiente de atrito cinético entre o blocoB e o plano horizontal é μ k=0,50 . O ângulo do plano inclinado sem a
Uma cômoda com uma massa de 45k g , incluindo as gavetas e as roupas, está em repouso sobre o piso. (a) Se o coeficiente de atrito estático entre a cômoda e o piso é 0,45 , qual é o módulo da menor fo
Em um jogo de shuffleboard improvisado, estudantes enlouquecidos pelos exames finais usam uma vassoura para movimentar um livro de cálculo no corredor do dormitório. Se o livro de 3,5k g adquire uma v