Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.3 - Ex. 13
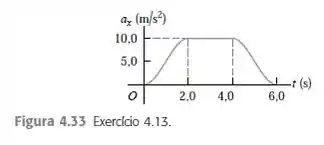
Uma carreta de brinquedo pesando está em aceleração por uma linha reta . O gráfico da figura mostra essa aceleração em função do tempo.
- Ache a força resultante máxima que atua sobre esse objeto. Quando essa força máxima ocorre?
- Em que instantes a força resultante sobre o objeto é constante?
Quando a força resultante é igual a zero?
Passo 1
Fala aí! como vai?
Nesse problema temos uma carreta de brinquedo pesando que está em aceleração por uma linha reta. O gráfico do enunciado mostra essa aceleração em função do tempo.
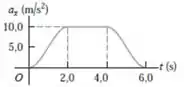
A partir daí temos que obter a força resultante máxima que atua sobre esse objeto e quando isso ocorre e tambem em que instantes a força resultante sobre o objeto é constante e quando a força resultante é igual a .
Parece complicado?
Para resolver esse problema temos que aplicar a segunda lei de Newton
Veja só!
Passo 2
(a) A força resultante máxima ocorre onde a aceleração aplicada for máxima. Isso por causa da segunda lei de Newton, onde a força resultante é:
Pelo gráfico, temos que a aceleração parte do zero e vai aumentando de valor. Atinge um valor máximo de no instante , permanece com esse valor máximo até o instante e depois vai gradativamente diminuindo de valor, até voltar ao zero.
E a força? Ela segue o mesmo ritmo da aceleração: vai ser máxima entre os instantes e . E seu valor? Bom, aqui entra a segunda lei de Newton de novo:
Como a massa do objeto é de e a aceleração máxima é então a força máxima vai ser:
Tranquilo até aqui?
Passo 3
(b) A força resultante, como comentei ali em cima, segue o mesmo ritmo da aceleração. Então temos que entre os instantes e a aceleração é constante, consequentemente, a força nesse intervalo também será constante.
Show?
Passo 4
(c) E quando a força resultante é zero? Ela vai ser zero quando a aceleração for zero. No gráfico isso ocorre nos instantes e .
E aí! entendeu tudo? Responde Aí!
