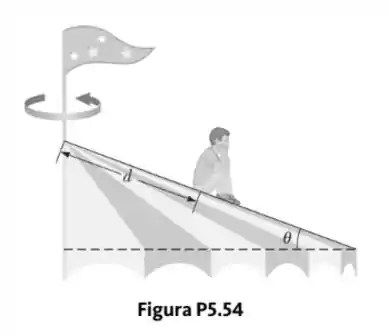
Por que a seguinte situação é impossível? Uma criança travessa vai a um parque de diversões com sua família. Em um brinquedo, depois de levar uma bronca da mãe, ela escorrega do seu assento e sobe para o topo da estrutura do brinquedo, que tem forma de cone com eixo vertical e lados inclinados que fazem um ângulo de com a horizontal, como mostrado na Figura P5.54. Esta parte da estrutura gira sobre o eixo central vertical quando o brinquedo é operado. A criança se senta na superfície inclinada em um ponto para baixo do lado inclinado a partir do centro do cone e faz biquinho. O coeficiente de atrito estático entre ela e o cone é . O operador não nota que a criança saiu de seu assento e então continua operando o brinquedo. Como resultado, a criança amuada sentada gira em uma trajetória circular a uma velocidade de .
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
O diagrama de corpo livre é mostrado abaixo:
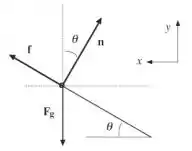
Onde é assumido que o atrito aponta para cima da inclinação, caso contrário, a criança iria deslizar para baixo na inclinação. A força líquida é direcionada para a esquerda em direção ao centro do caminho circular em que a criança percorre. O raio desse caminho é .
Três forças agem sobre a criança, uma força normal, atrito estático e gravidade. As relações de seus componentes de força são:
Passo 2
Resolva o atrito estático e a força normal.
Para resolver o atrito estático, multiplique a equação [1] pore a equação [2] por e adicione:
Para resolver a força normal, multiplique a equação [1] por e a equação [2] por e adicione:
Acima, nós usamos .
Se as equações acima devem ser consistentes, o atrito estático e a força normal devem satisfazer a condição , isso significa:
Passo 3
Usando este resultado, e que , temos o requisito de:
Se esta condição não for atendida, se v for muito grande, a situação física não pode existir.
Os valores dados no problema são . Verifique se o valor dado de v satisfaz a condição acima:
A situação é impossível porque a velocidade da criança dada no problema é muito grande: o atrito estático não conseguiu manter a criança no lugar na inclinação.
Resposta
Ver resolução