Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 126
Um carrinho de criança, com rodas sem atrito, é puxado por uma corda sob uma tensão T. A massa do carrinho é . Uma carga de massa está em cima do carrinho, com um coeficiente de atrito estático entre o carrinho e a carga. O carrinho é puxado para cima de uma rampa inclinada de um ângulo acima da horizontal. A corda é paralela à rampa. Qual é a máxima tensão T que pode ser aplicada sem carga deslize?
Passo 1
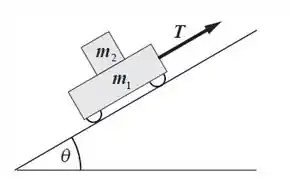
Para a aceleração ser máxima sem que a carga deslize sobre o carrinho, a força de atrito entre a carga e o carrinho tem que ser máxima, ou seja . Vamos fazer a segunda lei de Newton no sistema composto pelo carrinho e pela carga:
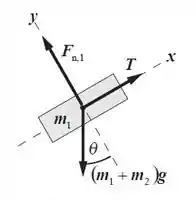
Passo 2
Agora a segunda lei de Newton na carga:
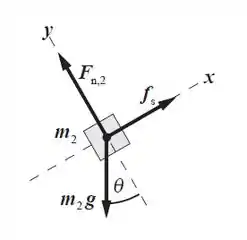
Passo 3
Agora em x, na carga:
Só que :
Joga (2) em (3):
Isola :
Passo 4
Agora joga (4) em (1):
Resposta
Exercícios de Livros Relacionados
Em um dia de inverno gelado, o coeficiente de atrito entre os pneus de um carro e uma estrada é reduzido para um quarto de seu valor em um dia seco. Como resultado, a velocidade máxima v m á xs e c o
Projetando sua nova casa na Califórnia (nos Estados Unidos, em região geologicamente instável), você a prepara para suportar uma aceleração horizontal máxima de 0,50 g . Qual é o menor coeficiente de
Você está fazendo voar um aeromodelo de 0,400k g de massa, preso a um cordão horizontal. O avião deve voar em um círculo horizontal de 5,70m de raio, (Suponha o peso do avião compensado pela força de
Um bloco de 45k g desliza para baixo, em um plano inclinado que forma um ângulo de 28 ° com a horizontal. Partindo do repouso, o bloco desliza uma distância de 2,4m em 5,2s . Encontre o coeficiente de