Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 125

Em um parque de diversões, você está sentado em um banco de um compartimento que gira com rapidez constante em um círculo vertical de 5,0 m de raio. O brinquedo é planejado de forma que sua cabeça está sempre apontando para o centro do círculo. (a) Se uma volta completa é efetuada em 2,0 s, encontre a orientação e a magnitude de sua aceleração. (b) Encontre a menor taxa de rotação (em outras palavras, o maior tempo T m para fechar um circulo) para a qual o cinto de segurança não exerce nenhuma força sobre você no ponto mais alto da volta.

Passo 1

Letra (a)

Como a velocidade é constante, não tem aceleração tangencial. A aceleração é só centrípeta:

a c = v 2 r

Só que a velocidade tem uma expressão conhecida:

v = 2 π r T

Agora pega a expressão da velocidade e joga na equação de cima:

a c = 2 π r T 2 r = 4 π 2 r 2 T 2 ∙ 1 r

a c = 4 π 2 r T 2

Passo 2

Agora a gente substitui os valores:

a c = 4 π 2 ( 5,0   m ) 2,0   s 2

a c = 49   m / s 2

Passo 3

Letra (b)

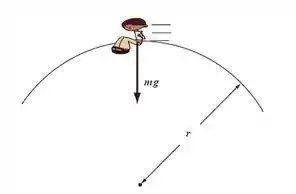
Se o cinto não exerce força, a força centrípeta é dada só pelo peso:

F c = m g

m v 2 r = m g

v 2 = g r ⇒ v = g r             E q .   1

Passo 4

O período se relaciona com a velocidade pela fórmula:

T m = 2 π r v             E q .   2

Joga a equação 2 na equação 1:

T m = 2 π r g r = 2 π r g

Passo 5

A questão quer a taxa de rotação, ou seja, frequência. Só que frequência é o inverso do período:

f = 1 T m = 1 2 π g r

Agora substitui os valores:

f = 1 2 π 9,8   m / s 2 5,0   m = 0,22   H z

Resposta

Letra (a): 49   m / s 2

Letra (b): 0,22   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aeromodelo de massa 0,750k g voa com uma velocidade de 35,0m / s em um círculo horizontal na ponta de um fio de controle de 60,0m de comprimento, como mostrado na Figura P5.57a. As forças exercidas
Um brinquedo em um parque de diversões consiste em um cilindro vertical muito grande que gira sobre seu eixo com velocidade suficiente para que qualquer pessoa dentro seja mantida contra a parede quan
Uma criança está treinando para uma corrida de BMX. Sua velocidade permanece constante enquanto ela vai em sentido anti-horário em uma pista com duas seções retas e duas quase semicirculares, como mos
Uma montanha-russa no parque de diversões Six Flags Great America em Gurnee, Illinois, incorpora algumas tecnologias inteligentes e um pouco de física básica. Cada loop vertical, em vez de ser circula
65. Uma mola leve tem comprimento não distendido de 15,5c m . Ela é descrita pela lei de Hooke com constante elástica de 4,30N / m . Uma extremidade da mola é mantida sobre um eixo vertical fixo e a o