Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 101
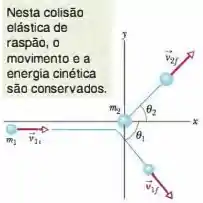
No arranjo da Fig. 9-21, a bola de sinuca 1, que se move a , sofre uma colisão oblíqua com a bola de sinuca 2, que está inicialmente em repouso. Após a colisão, a bola 2 se move com uma velocidade escalar de e um ângulo . Quais são (a) o módulo e (b) a orientação da velocidade da bola 1 após a colisão? (c)Os dados fornecidos mostram que a colisão é elástica ou inelástica?
Passo 1
Bom pessoal , vamos chamar a massa das bolas de , a velocidade inicial da bola 1 de , a velocidade final da bola 1 de e a velocidade final da bola 2 de . Aplicando a lei de conservação do momento linear às componentes e , temos que :
Como a massa pode ser cancelada nas duas equações, ficamos com duas equações e duas incógnitas, o que nos permite calcular os valores de e .
Passo 2
Resolvendo o sistema de equações acima, obtemos que :
Para , e , temos:
o que nos dá .
A velocidade da bola 1 após a colisão , por sua vez , é dada por :
Passo 3
De acordo com os resultados do item anterior e a figura fornecida pelo problema , concluímos que no sentido horário em relação ao semieixo positivo.
Passo 4
Bom pessoal , a energia cinética antes da colisão é . Após a colisão, temos que :
Substituindo as expressões de e determinadas no item (a), temos que :
Como e , e . Nesse caso, , o que mostra que a colisão é elástica, já que a energia mecânica é conservada.
Resposta
A colisão é elástica .
Tranquilo galera? Bora resolver mais questões então