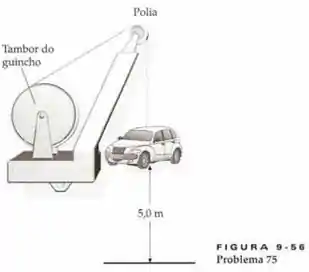
Um carro de está sendo retirado da água por um guincho. No momento em que o carro está acima da água, a caixa de engrenagens quebra e o tambor do guincho gira livremente enquanto o carro cai. Durante a queda do carro, não existe deslizamento entre a corda (sem massa), a polia e o tambor. O momento de inércia do tambor do guincho é e o momento de inércia da polia é . O raio do tambor é e o raio da polia é . Suponha o carro partindo do repouso. Determine a rapidez com que ele atinge a água.

Vamos considerar que nosso referencial de altura é a água.

Quando o carro de massa está na altura , ele está parado. Então ele não tem energia cinética, apenas potencial gravitacional .

E nesse momento, o tambor e a polia estão parados também, porque eles só giram quando o carro se move, então a energia cinética de rotação dele é nula.

Logo, a energia do sistema nesse momento é somente a energia do carro, dada por

Como o carro é o único que muda de altura na situação, a gente só olha a energia potencial gravitacional dele, tudo bem?

Já quando o carro chega na água, a altura dele é nula, então não há energia potencial gravitacional.

Mas o carro está em movimento com velocidade , e por isso ele tem energia cinética:

E como o carro se move, a polia e o tambor também começam a girar. E se eles giram, eles têm rapidez angular, e por isso, têm energia cinética de rotação. A fórmula dessa energia é

Se é a massa da polia e a do tambor, e é o momento de inércia da polia e o momento de inércia do tambor, a polia tem essa energia

E o tambor tem

Logo a energia final total é

Então pela conservação de energia:

Como o tambor e a polia rodam sem deslizar e eles rodam por causa da corda que tem a mesma velocidade linear do carro, a gente pode relacionar a rapidez angular da polia e do tambor com a rapidez linear do carro assim:

Então para a polia vamos ter e para o tambor . Substituindo na nossa equação:

Agora é isolar quem a gente quer, a rapidez

Substituindo valores: