O sistema mostrado na figura consiste em um bloco de colocado sobre uma prateleira horizontal sem atrito. Este bloco está preso a um cordão que passa por uma polia e tem sua outra extremida presa a um bloco pendente . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

Passo 1
Oláaa, querido! Tá bem?
Ele quer as tensões na corda e a aceleração dos blocos. A aceleração vai ser a mesma para os dois blocos, porque eles estão ligados pela corda e ela não pode arrebentar ou ficar frouxa.
Já a tensão vai ser diferente para cada extremidade porque a gente vai considerar a massa da polia.
E como a gente quer achar forças e aceleração, podemos aplicar a segunda lei de Newton para cada objeto do sistema para encontrar as equações que descrevem o movimento dos blocos.
E se tem segunda lei de Newton na história, precisamos fazer o diagrama do corpo livre para cada objeto. Ficam assim:
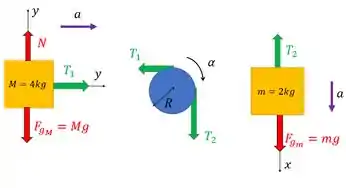
Colocamos o positivo no sentido da aceleração.
Passo 2
Vamos aplicar a segunda lei de Newton para o bloco de massa .
No eixo vamos ter:
A aceleração nessa direção é a aceleração que a gente quer descobrir, então . E nessa direção só temos . Logo a segunda lei de Newton fica:
Passo 3
Agora vamos olhar para o bloco de massa . Só temos forças na direção :
Aí temos . Substituindo isso e as forças com seus devidos sinais representando seus sentidos em relação ao nosso referencial:
Sendo que :
Passo 4
Quase lá, bora!
Só falta aplicar a segunda lei de Newton na polia. Mas repara que a gente não colocou eixos e nela. É porque a polia está girando, então a gente vai aplicar a segunda lei de Newton para a rotação. O sentido positivo é o sentido da aceleração angular representada.
Temos que a segunda lei de Newton para rotação é
Os torques causados pelas tensões sobre a polia vão ser o produto entre a tensão e o raio da polia, já que o eixo de rotação é o centro dela. Então temos:
Repara que gera torque no sentido de , por isso ele fica positivo e (que gera torque no sentido contrário) fica negativo.
Esse é o momento de inércia da polia. Ela é basicamente um disco de raio e massa . O momento de inércia de um disco em relação a um eixo que passa pelo seu centro é
Substituindo na nossa equação:
E essa aceleração angular pode ser reescrita em função da aceleração linear a borda do disco usando essa expressão:
Nossa equação fica:
Passo 5
Agora é relacionar as equações que a gente achou para achar expressões para , e .:
Vamos substituir e em :
Isolando
Substituindo valores numéricos:
Passo 6
Com o valor de , a gente pode voltar em e e achar nossas tensões.
Temos:
Então a tensão 1 fica:
E a tensão 2: