Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 68

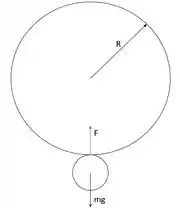
Um disco uniforme, de massa M e raio R , pode girar livremente em torno de um eixo fixo horizontal que passa pelo seu centro de massa perpendicularmente ao seu plano. Uma pequena partícula de massa m é presa à borda do disco no topo, diretamente acima do pivô. O sistema é levemente desesquilibrado e o disco começa a girar. Quando a partícula passa pelo seu ponto mais baixo, (a) qual é a rapidez angular do disco e (b) qual é a força exercida pelo disco sobre a partícula?

Passo 1

À primeira vista essa situação é bem esquisita. Eu demorei bastante pra entender como era pra ser o desenho. O disco vai rodar ao redor do eixo que passa pelo seu centro, e a bolinha menor fica pendurada nele!

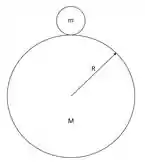
Aaaah, agora entendi, agora eu saquei!!!

Passo 2

  1. Conservando energia do ponto mais alto até o ponto mais baixo:

    2. E r o t a ç ã o = m g Δ h

    1 2 I d i s c o ω 2 + 1 2 I b o l a ω 2 = m g Δ h

    ω = 2 m g Δ h I d i s c o + I b o l a

    ω = 2 m g ( 2 R ) 1 2 M R 2 + m R 2

    ω = 8 m g R ( 2 m + M )

    Passo 3

  2. A força centrípeta é igual à resultante das forças no ponto mais baixo:

F - m g = m ω 2 R

F = m g + m ω 2 R

F = m g + m R 8 m g R 2 m + M

F = m g 1 + 8 m 2 m + M

Resposta

  1. ω = 8 m g R ( 2 m + M )
  2. F = m g 1 + 8 m 2 m + M
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Big Ben, o relógio da torre do Parlamento em Londres, tem o ponteiro menor (da hora) com 2,70m de comprimento e massa de 60,0k g , e o ponteiro maior (do minuto) com 4,50m de comprimento e massa de 10
Barras rígidas de massas desprezíveis localizadas ao longo do eixo y conectam três partículas (Fig.P10.18). O sistema gira no eixo x com velocidade angular de 2,00r a d / s . Encontre o momento de iné
Este problema descreve um método experimental para determinar o momento de inércia de um corpo de formato irregular tal como a carga de um satélite. A Figura P10.38 mostra um contrapeso de massa m sus
Um cilindro de massa 10,0k g rola sem escorregar em uma superfície horizontal. Em certo instante, seu centro de massa tem velocidade de 10,0m / s . Determinea energia cinética translacional do centro
Um disco sólido e um aro uniformes são colocados lado a lado no topo de uma rampa de altura h . Se os dois são liberados do repouso e rolam sem escorregar, qual deles chega primeiro à base?Verifique s