Um carro de , viajando para o norte a , colide em um cruzamento com um carro de que viaja para o oeste a . Os dois carros ficam presos um ao outro. (a) Qual é a quantidade de movimento total do sistema antes da colisão? (b) Quais são a magnitude e a orientação da velocidade do conjunto justo após a colisão?
Passo 1
a) Oláaa, cê tá bem?
Então, temos aqui um objeto batendo em outro, e a partir daí andando juntos, mostrando uma colisão inelástica. Vamos considerar o norte como o positivo e o leste como o positivo e anotar os dados:
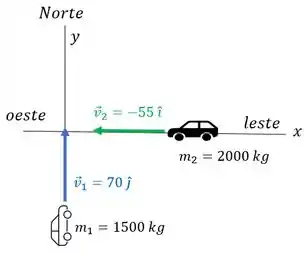
é negativa porque aponta para o sentido negativo de . Como eles ficam juntos depois da colisão, a velocidade final deles é igual.
E o enunciado quer saber a quantidade de movimento total do sistema antes da colisão. Vamos calcular isso aí!
Passo 2
Olha, a quantidade de movimento é calculada assim:
Aí para calcular a quantidade de movimento total de um sistema, a gente calcula para cada objeto do sistema e soma. Então, para o nosso caso, a quantidade de movimento total inicial vai ser a soma de do carro 1 com do carro 2
Percebe que usamos as velocidades antes da colisão porque queremos a quantidade de movimento antes da colisão.
Como todas as velocidades estão em km/h, não tem problema usarmos os valores como estão. Então a gente pode substituir nossos dados aí:
Passo 3
b) E o enunciado quer a magnitude de e sua orientação.
Aqui te dou a dica master: falou de achar velocidade de objetos depois da colisão, pensa em conservação da quantidade de movimento. É isso que vamos usar para achar . A conservação diz que
Ou seja, a quantidade de movimento antes e depois da colisão devem ser iguais.
A gente já tem a quantidade . Então vamos achar a expressão de . Depois da colisão, os carros se movem juntos, então podemos pensar que temos um objeto só de massa , se movendo com velocidade . Ficamos com
Substituindo isso e na equação da conservação:
Substituindo os dados:
Passo 4
Temos então essas componentes de :
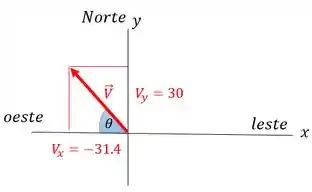
O módulo (magnitude) da velocidade é:
Pela figura, vemos que o ângulo da direção dos carros após a batida com oeste () será dado pela fórmulinha:
Portanto, o carro viaja na direção noroeste, formando com a parte negativa de .
Resposta
a)
b) O carro viaja na direção noroeste, formando com oeste.