Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 21
Um carro de derrapa até parar sobre o piso molhado de uma rodovia em que . Com que rapidez o carro estava se deslocando se ele percorre durante a derrapagem?
Passo 1
Vamos desenhar a situação e as forças que atuam sobre o carro:
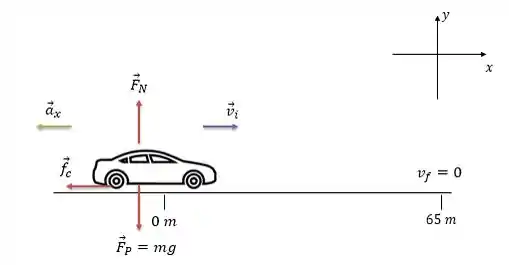
Vamos assumir que o carro começa a derrapar na posição com uma velocidade inicial . O carro para, ou seja, atinge velocidade final na posição . Para que a velocidade do carro vá diminuindo é necessário que tenha uma aceleração resultante, , no sentido contrário do movimento.
As forças que atuam no carro são a força peso, força normal e a força de atrito cinético, no sentido contrário do movimento.
Passo 2
É justamente a força de atrito cinético no sentido contrário do movimento que é responsável pela aceleração, que vai “frear” o carro, porque ela é a única força na direção .
Aplicando a primeira e segunda Lei de Newton:
Sabendo a fórmula para a força de atrito:
Podemos reescrever a equação:
Passo 3
Agora precisamos saber o módulo da força normal. Como o carro não se movimenta verticalmente, na direção , o somatório de força nessa direção tem que ser zero:
Substituindo o módulo da força normal na equação encontrada no passo 2, temos:
O coeficiente foi fornecido na questão e a aceleração da gravidade nós conhecemos:
Então:
Passo 4
Agora que conhecemos a aceleração precisamos encontrar uma equação para acharmos a velocidade inicial. Pensa aqui comigo, nós sabemos a velocidade final, a aceleração e temos a distância percorrida pelo carro, mas não temos nenhuma informação do tempo que o carro levou para parar, não é?
Lembra que tem uma equaçãozinha que descreve o movimento e que é independente do tempo?
Isso aí, a equação de Torricelli:
Isolando :
As informações que temos são:
Agora só substituir e achar a :
Terminamos =)
Resposta
O carro estava se deslocando com uma velocidade inicial .