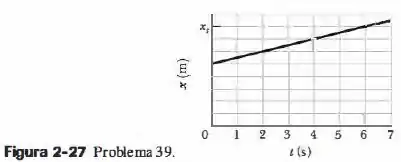
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição do carro é dada na Fig., do instante ao instante . A escala vertical do gráfico é definida por . Em , o carro está em , com uma velocidade de e uma aceleração negativa · (a) Qual deve ser o valor de para que os carros estejam lado a lado (ou seja, tenham o mesmo valor de em ? (b) Para esse valor de, quantas vezes os carros ficam lado a lado? (c) Plote a posição do carro em função do tempo na Fig. . Quantas vezes os carros ficariam lado a lado se o módulo da aceleração fosse (d) maior do que o da resposta do item (a) e (e) menor do que o da resposta do item (a)?

Para saber quantas vezes os carros ficam lado a lado temos que encontrar a função posição para e .

A velocidade de é igual o coeficiente angular da reta que define sua posição, de até a distância de A varia de até e por esse motivo .

Igualando as duas equações temos:

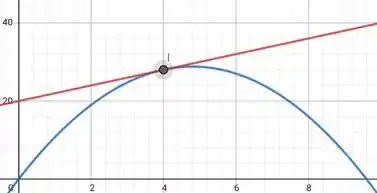
Como a equação só possui uma raiz e isso prova que só em um único ponto.

Gráfico de em vermelho e gráfico de em azul, o ponto é a interseção entra eles.

Para valores de não há interseção e para valores de há duas interseções.