Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 86

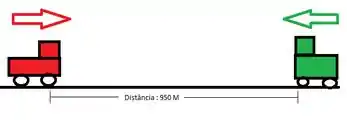
Um trem vermelho a 72   k m / h e um trem verde a 144   k m / h estão na mesma linha, retilínea e plana, movendo-se um em direção ao outro. Quando a distância entre os trens é 950   m , os dois maquinistas percebem o perigo e acionam os freios, fazendo com que os dois trens sofram uma desaceleração de 1,0   m / s 2 . Os trens conseguem frear a tempo de evitar uma colisão? Caso a resposta seja negativa, determine as velocidades dos trens no momento da colisão; caso seja positiva, determine a distância final entre os trens.

Passo 1

Para começar vamos analisar o enunciado, observem que a questão deixa claro que os dois trens estão na mesma linha e que ambos possuem uma desaceleração constante, ou seja, é um problema de MRUV.

Para saber se haverá uma colisão é necessário saber a distância pecorrida por cada trem até parar, para isso temos a fórmula da função horária da posição:

x ( t ) = x 0 + v 0 t +   1 2 a t 2 onde:

s = p o s i ç ã o ; s 0 = p o s i ç ã o   i n i c i a l ; v 0 = v e l o c i d a d e   i n i c i a l ; t = t e m p o ; a = a c e l e r a ç ã o .

Passo 2

Para prosseguir devemos extrair e separar os dados das questões:

Dados trem vermelho ( V 1 )

Velocidade Inicial: V 0 = 72 k m / h

Dados trem verde ( V 2 )

Velocidade Inicial: V 0 = 144 k m / h

Distância de 950   m ; Desaceleração de a = - 1,0 m / s 2

OBS: Necessário observar as grandezas do problema, observe se há necessidade de conversão.

Passo 3

Devemos observar que a velocidade é dada em k m / h e aceleração em m / s 2 , sendo assim, necessita ser convertida para k m / h ou   m / s para deixar no SI.

V 1 = 72 k m h = 72 × 1000 m 3600 s = 72000 m 3600 s = 20   m / s

V 2 = 144 k m h = 144 × 1000 m 3600 s = 144000 m 3600 s = 40   m / s

Passo 4

Analisando a fórmula da função horária da posição em função do tempo percebemos que nos falta uma variável, o tempo. A equação que podemos utilizar nesse caso para determinar essa variável é a função da velocidade, v = v 0 + a t . Assim:

v 1 = v 0 + a t

0 = 20 + - 1 t

t = 20   s e g u n d o s

v 2 = v 0 + a t

0 = 40 + - 1 t

t = 40   s e g u n d o s

Passo 5

Após acharmos todas as variáveis, utilizaremos a principal fórmula do nosso problema:

x ( t ) = x 0 + v 0 t +   1 2 a t 2

s 1 = 0 + ( 20 × 20 ) + ( ( - 1 ) × ( 20 ) 2 ) 2

s 1 = 400 - 200 = 200   m

Portanto, s 1 = 200   m é a distância percorrida pelo trem vermelho.

s 2 = 0 + ( 40 × 40 ) + ( ( - 1 ) × ( 40 ) 2 ) 2

s 2 = 1600 - 800

s 2 = 800   m  

Portanto, s 2 = 800   m é a distância percorrida pelo trem verde.

Observe que haverá colisão, a soma das duas distância equivalem a 1000   m e a distância dada pelo problema é de 950   m .

Passo 6

No momento do impacto, o trem vermelho estará parado.

O trem verde estará com a velocidade de 10   m / s , observe o cálculo utilizando a Equação de Torricelli:

V 2 = V 0 2 + 2 a ∆ x

V 2 = ( 40 ) 2 + 2 ( - 1 ) ( 950 - 200 )

V 2 = 1600 - 1500

V 2 = 100

V = 100 = 10   m / s

Resposta

  1. N ã o   e v i t a m   a   c o l i s ã o .
  2. v v e r m e l h o = 0   m / s e v v e r d e = 10   m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas de 72 a 75 , lhe são fornecidas uma ou mais equações cinemáticas para usar na resolução de um problema. Para cada um deles, você deve: a . Redigir um problema realista para o qual esta o
79. Medições muito acuradas são feitas durante a corrida olímpica de 100m e t r o s rasos. Um modelo simples, mas razoável, da aceleração de um corredor revela que este se acelera a 3,6m / s ² ² duran
58 . Um trem de brinquedo é empurrado para a frente e é solto em x 0=2,0m com uma rapidez de 2,0m / s . Ele rola com velocidade constante durante 2,0s e depois começa a perder velocidade. Ele atinge o
59 . Bob está dirigindo o carro de fuga depois de um grande assalto a banco. Ele está trafegando a 50m / s quando seus faróis revelam subitamente um tapete de pregos que os policiais colocaram na estr
54 . Um carro acelera a 2,0m / s 2 ao longo de uma estrada retilínea. Ele passa por duas placas separadas por 30 m nos instantes t = 4 , 0 s e t = 5,0 s . Qual é a velocidade do carro em t = 0 s ?