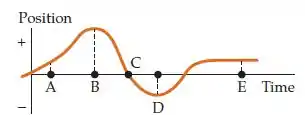
O diagrama na figura abaixo mostra a localização de um objeto se movendo em uma linha reta ao longo do eixo . Considere que o objeto está na origem em . Dos cinco tempos mostrados, qual(is) tempo(s) representam o objeto quando está (a) mais distante da origem, (b) em repouso por um instante, (c) em um breve intervalo de repouso e (d) se movendo para longe da origem?

(b) O objeto está em repouso (por um instante) nos pontos em que a sua velocidade é nula.

A velocidade é dada por

Essa expressão representa a inclinação da nossa curva no gráfico. Para se aular, a inclinação do gráfico deve ser zero, ou seja, a curva deve estar paralela à horizontal.

Quando isso acontece? Onde a gente tem montes ou vales no gráfico. Para a gente, isso acontece nos pontos e .

(c) O objeto está em um intervalo de repouso no ponto , pois ele está localizado em um trecho horizontal, em que a condição que mencionamos ali em cima:

é satisfeita para vários pontos. No trecho em torno do ponto , a velocidade do objeto é nula em muitos pontos consecutivos, e por isso a posição não muda durante esse intervalo.

(d) Para responder essa, a gente precisa olhar para os pontos ao redor do nosso ponto, ou seja, para os pequenos intervalos onde nossos pontos estão. O objeto está se movendo para longe da origem nos intervalos em que, restritamente, aumenta, e aumenta em módulo.

Como assim? Nos instantes onde os pontos da nossa curva ficam cada vez mais distantes da origem em relação ao eixo vertical, conforme o tempo passa, e assim, ficam cada vez mais distante do eixo horizontal. Seja indo para baixo ou seja indo para cima.

Isso acontece no ponto , porque está aumentando, e a distância do objeto em relação a origem está aumentando. Isso porque o valor de está aumentando em módulo (ficando mais distante da origem em relação ao eixo vertical).

Percebe que isso também serve para , por que?

Porque nele, conforme aumenta, o valor da posição vai se tornando cada vez maior negativamente, ou seja, vai aumentar em módulo. E os pontos da curva vão ficando cada vez mais distantes do eixo horizontal, ou seja, distantes da origem do eixo vertical, que representa ao origem da posição.