Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 2º - Capítulo 10.Problemas - Ex. 14

(Casamento de impedâncias) No circuito da figura ,   Z   =   R   +   i X é a impedância interna do gerador de corrente alternada de voltagem V   e   Z '   =   R '   +   i X ´ a impedância alimentada pela corrente I do gerador. Demonstre que a potência transferida a Z ´ é máxima quando

Z ' = Z * = R - i X

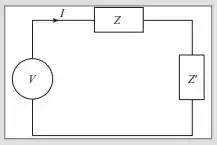
Assim, se X corresponde a uma reatância capacitiva ,   X ' corresponde a uma reatância indutiva, e vice-versa. Se as reatâncias são desprezíveis, basta que as resistências sejam iguais.

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de eletromagnetismo do Moysés dado o circuito da figura ,   Z   =   R   +   i X é a impedância interna do gerador de corrente alternada de voltagem V   e   Z '   =   R '   +   i X ´ a impedância alimentada pela corrente I do gerador. Demonstre que a potência transferida a Z ´ é máxima quando

Z ' = Z * = R - i X

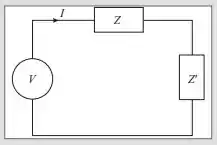
Assim, se X corresponde a uma reatância capacitiva ,   X ' corresponde a uma reatância indutiva, e vice-versa. Se as reatâncias são desprezíveis, basta que as resistências sejam iguais.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha nessa questão ele deseja determinar a reatância indutiva dado o circuito,

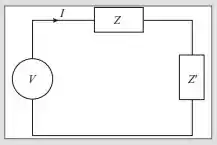
Definido por,

Z   =   R   +   i X           e       Z '   =   R '   +   i X ´

Sendo,

Z T = Z 1 Z + Z 2 ( Z 1 2 + Z T ) Z 1 2 + Z T + Z 2

Ficando sua definição,

Z T     Z 1 2 + Z r 2 + Z T Z 2 = Z 1 2 2 + Z 1 Z T 2 + Z 2 Z Z

Chegando em,

Z T = Z 1 2 2 + Z T Z 2 + Z 1

Temos,

Z T = Z 1 Z 2 + 1 4 Z 1 2 = Z 1 Z 2   1 + Z 1 4 Z 2

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

Z 1 Z 2   1 + Z 1 4 Z 2

Exercícios de Livros Relacionados

As duas bobinas da figura 30-72 têm indutâncias L 1 e L 2 quando estão muito afastadas. A indutância mútua é M . (a) Mostre que a combinação que aparece na figura pode ser substituida por uma indutânc
A bobina 1 tem L 1 = 25m H e N 1 = 100 espiras. A bobina 2 tem L 2 = 40m H e N 2 = 200 espiras. As bobinas são mantidas fixas no espaço; a indutância múta é 3,0m H . Uma corrente de 6,0m A na bobina 1
Dois solenoides fazem parte do circuito de ignição de um automóvel. Quando a corrente em um dos solenoides diminui de 6,0A para zero em 2,5m s , uma força eletromotriz de 30k V é induzida no outro sol
A bobina 1 tem L 1 = 25m H e N 1 = 100 espiras. A bobina 2 tem L 2 = 40m H e N 2 = 200 espiras. As bobinas são mantidas fixas no espaço; a indutância múta é 3,0m H . Uma corrente de 6,0m A na bobina 1
Uma bobina C de N espiras envolve um solenoide longo S de raio R e n espiras por unidade de comprimento, como na figura 30-67. (a) Mostre que a indutância mútua da combinação bobina-solenoide é dada p