Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 12c

Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidade de carga (fig.).

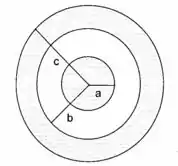
Calcule o campo elétrico na região b ≤ r ≤ c .

Passo 1

Se liga! Para calcular o campo elétrico, aqui a maneira mais simples de fazer é aplicando a lei de Gauss

ϕ = E A = q i n t ϵ 0

Estamos interessados na região b ≤ r ≤ c .

Passo 2

Mas olha a figura:

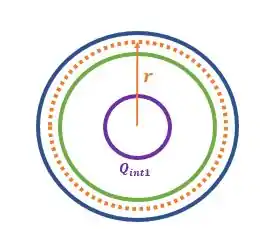
Assim se já sabemos que o módulo da carga interna na esfera maciça de raio a é igual a:

Q i n t 1 =   4 3 π ρ a 3

Queremos saber quanto de carga iremos envglobar a mais com essa parcela da casca esférica. Ou seja, vamos integrar a densidade volumétrica de carga ρ do raio menor da casca esférica b até o raio que desejamos r para encontrar a carga:

Q i n t 2 =   ∫ b r ρ   .   d v = 4 3 π . ρ .   ( r 3 - b 3 )

Passo 3

Logo a soma da carga interna dentro dessa superfície gaussiana que marcamos ( b ≤ r ≤ c ) possui uma carga interna total igual a:

Q t o t a l = Q i n t 1 + Q i n t 2  

Q t o t a l = 4 3 π ρ a 3 + 4 3 π . ρ .   ( r 3 - b 3 )

Simplificando:

Q t o t a l =   4 3 π ρ ( r 3 + a 3 - b 3 )

E qual é a área da superfície gaussiana? Simples, é área de uma esfera de raio r :

A = 4 . π . r 2

Passo 4

Logo, como E A = q i n t ϵ 0 :

E = 4 3 π ρ r 3 + a 3 - b 3 ϵ 0   .   ( 4 . π . r 2 )  

Simplificando, temos:

E = ρ r 3 + a 3 - b 3 3 .   ϵ 0   .   r 2

Resposta

E = ρ r 3 + a 3 - b 3 3 .   ϵ 0   .   r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o fluxo elétrico através de uma superfície fechada por igual o zero, o campo elétrico deve ser zero em todos os pontos desta superfície? Se a reposta for não, dê um exemplo específico. A partir da
Explique por que a intensidade do campo elétrico aumenta linearmente com r no lugar de decrescer com inverso de r 2 entre o centro e a superfície de uma esfera sólida carregada uniformemente.
Verdadeiro ou falso:O campo elétrico devido a uma fina casca esférica oca, uniformemente carregada, é zero em todos os pontos no interior da casca. Em equilíbrio eletrostático, o campo elétrico em qua
Verdadeiro ou falso: A lei de Gauss vale apenas para distribuições simétricas de carga. O resultado que E = 0 para todos os pontos no interior do material de um condutor em condições eletrostáticas po
Medidas cuidadosas do campo elétrico na superfície de uma caixa preta indicam que o fluxo elétrico resultante saindo da superfície da caixa é 6,0k N ⋅ m 2 / C . (a) Qual é a carga resultante dentro da