Uma tradicional experiência de laboratório de física básica, que trata da conservação de energia e das leis de Newton, é mostrada na Figura 7-57. Um carrinho deslizante é colocado sobre um trilho de ar e é preso por um fio que passa por uma polia sem atrito e sem massa, a um peso pendente. A massa do carrinho é , enquanto a massa do objeto pendente é . Quando o colchão de ar é formado, o trilho se torna praticamente sem atrito. Então, você larga o objeto pendente e mede a rapidez do carrinho depois de o objeto ter caído uma certa distância . (a) Para mostrar que a rapidez medida é a prevista pela teoria, aplique conservação de energia mecânica e calcule a rapidez como função de (b) Para confirmar este cálculo, aplique a segunda e a terceira leis de Newton diretamente, esboçando um diagrama de corpo livre para cada uma das duas massas e aplicando as leis de Newton para determinar suas acelerações. Então, use a cinemática para calcular a rapidez do carrinho como função de

Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado já nos dá o passo a passo que deve ser seguido para resolver nosso problema, então vamos só aplicar.
Aplicando o teorema do trabalho e energia para a situação, temos:
Como é nulo, temos que:
A variação de energia mecânica é dada por:
Que representam a variação das parcelas cinéticas e potenciais.
O corpo parte do repouso, então sua parcela de energia cinética inicial é nula, . Temos também que , portanto:
Substituindo pelas respectivas fórmulas, temos:
A velocidade, será:
Passo 2
Item (b):
O diagrama de corpo livre de cada massa está expresso na figura abaixo:
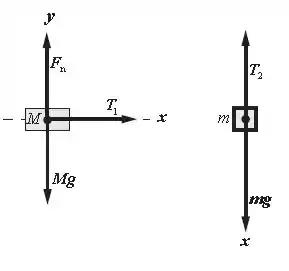
Aplicando a terceira lei de Newton, temos:
Aplicando a segunda lei de Newton em cada massa, temos:
Relacionando as duas equações, temos:
Usando uma equação para aceleração constante, temos:
Aplicando a condição de partir do repouso, temos:
Substituindo a equação da aceleração encontrada, temos:
Que é o mesmo resultado encontrado para o item (a).
Resposta
Ei, a resposta está no passo a passo :)