Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 102

Uma embarcação esportiva de 285   k g é dirigida, na superfície de um lago, com a rapidez constante de 13,5   m / s , de encontro a uma rampa inclinada de 25,0 ° acima da horizontal. O coeficiente de atrito entre o casco da embarcação e a superfície da rampa é 0,150 , e a extremidade mais elevada da rampa está 2,00   m acima da superfície da água. (a) Supondo que o motor é desligado quando a embarcação chega na rampa, qual é a sua rapidez ao abandonar a rampa? (b) Qual é a rapidez da embarcação quando ela atinge novamente a água? Despreze a resistência do ar.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A situação do enunciado pode ser descrita na figura abaixo:

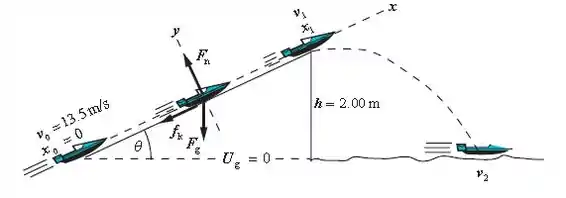
Aplicando o teorema do trabalho e energia, temos:

W e x t = ∆ E m e c + ∆ E t é r m

Como W e x t é nulo, temos que:

∆ E m e c + ∆ E t é r m = 0

A variação de energia mecânica é dada por:

∆ E m e c = ∆ K + ∆ U g

Que representam a variação das parcelas cinéticas e potenciais.

∆ E m e c = K 1 - K 0 + U g , 1 - U g , 0

Como a energia potencial no primeiro instante é nula, U g , 0 = 0 , temos que:

∆ E m e c = K 1 - K 0 + U g , 1

Substituindo pelas respectivas fórmulas, temos:

∆ E m e c = 1 2 m v 1 2 - 1 2 m v 0 2 + m g h

A variação da energia térmica é dada por:

∆ E t é r m = f k x 1 = μ k F n x 1

Como F n = m g cos ⁡ θ :

∆ E t é r m = μ k m g x 1 cos ⁡ θ

Substituindo no teorema, temos:

1 2 m v 1 2 - 1 2 m v 0 2 + m g h + μ k m g x 1 cos ⁡ θ = 0

Trigonometricamente, sabemos que x 1 = h sin ⁡ θ , portanto:

1 2 m v 1 2 - 1 2 m v 0 2 + m g h + μ k m g h sin ⁡ θ cos ⁡ θ = 0

A velocidade ao abandonar a rampa, v 1 , será:

v 1 = v 0 2 - 2 g h 1 + μ k cot ⁡ θ

Substituindo os valores, temos:

v 1 = 13,5 2 - 2 ⋅ 9,81 ⋅ 2 1 + 0,15 cot ⁡ 25 °

v 1 = 11,42   m / s

Passo 2

O item (b) nos pergunta qual a velocidade da embarcação quando ela atinge novamente a água. Bom, vamos usar o teorema do trabalho e energia novamente.

W e x t = ∆ E m e c + ∆ E t é r m

Agora, o trabalho externo e a variação de energia térmica são desconsiderados, pois também não temos atrito.

∆ E m e c = 0

A variação de energia mecânica é dada por:

∆ E m e c = ∆ K + ∆ U g

∆ E m e c = K 2 - K 1 + U g , 2 - U g , 1

Como a energia potencial no primeiro instante é nula, U g , 2 = 0 , temos que:

∆ E m e c = K 2 - K 1 - U g , 1

Substituindo pelas respectivas fórmulas, temos:

∆ E m e c = 1 2 m v 2 2 - 1 2 m v 1 2 - m g h

Substituindo no teorema, temos:

1 2 m v 2 2 - 1 2 m v 1 2 - m g h = 0

A velocidade ao atingir a água, v 2 , será:

v 2 = v 1 2 + 2 g h

Substituindo os valores, temos:

v 2 = 11,42 2 + 2 ⋅ 9,81 ⋅ 2

v 2 = 13   m / s

Resposta

a )   v 1 = 11,42   m / s

b ) v 2 = 13   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de 1500k g começa a descer, a 30k m / h , uma ladeira com uma inclinação de 5,0 ° . O motor do carro está desligado e as únicas forças presentes são a força de atrito exercida pela estrada e
Um bloco de 15k g sofre uma aceleração de 2,0m / s 2 em uma superfície horizontal sem atrito que faz sua velocidade aumentar de 10m / s para 30m / s . Qual é (a) a variação da energia mecânica do bloc
Dois picos nevados estão H=850m e h=750m acima do vale que os separa . Uma pista de esquiação, com um comprimento total de3,2k m e uma inclinação média θ=30 ° , liga os dois picos (Fig. 8-59). (a) Um
A resistência ao movimento de um automóvel é constituída pelo atrito da estrada, que é quase independente da velocidade, e o arrasto do ar, que é proporcional ao quadrado da velocidade. Para um certo
Um disco de shuffleboard de 0,42k g está em repouso quando um jogador usa um taco para imprimir ao disco uma velocidade de 4,2m / s com a aceleração constante. A aceleração ocorre em uma distância de