Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.7 - Ex. 50
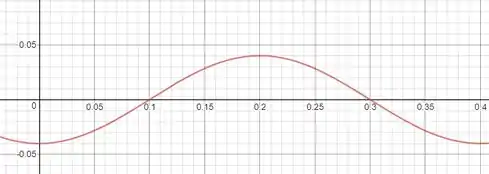
Uma certa onda estacionária transversal em uma corda longa possui um antinó em e um nó vizinho em . O deslocamento da partícula da corda situada em é mostrado na Figura, onde a escala do eixo é definida por . Para , qual é o deslocamento da partícula da corda situada ( a) em e (b) em ? Qual é a velocidade transversal da partícula situada em (c) no instante se (d) no instante ? (e) Plote a onda estacionária, no intervalo de a , para o instante .
Passo 1
Fala galerinha bonita, vamos começar! Nessa questão, como o enunciado nos pergunta quais são os deslocamentos de partículas localizadas em diferentes pontos da corda, primeiro, a gente precisa escrever a equação dessa onda estacionária.
Lembra do formato geral dessa equação? Ele é tipo isso:
tal que , e são a amplitude da onda, seu número de onda (igual a ) e sua frequência angular. Colocamos o sinal acima, pois ele depende do comportamento crescente ou decrescente inicial de com Na figura, a gente consegue ver que para um fixo, com o aumento de o começa a decrescer, ficando cada vez mais negativo para depois crescer. Então, como a função seno é crescente, dá pra deduzir que o sinal mais adequado é o de menos. Então a equação geral dessa onda estacionária é
Passo 2
Belezinha! Agora a gente já está quase preparado para matar a letra (a) e as seguintes. Mas antes a gente precisa descobrir qual são os valores de , e .
Eles podem ser descobertos diretamente a partir dos dados do enunciado. Primeiro, note que , que é a amplitude da onda. Da figura na questão, a gente pode perceber que o tempo que demora para a posição completar um ciclo é igual a . Então, e
Agora, pra gente descobrir a gente precisa prestar atenção entre as distâncias de alguns pontos localizados em posições diferentes dadas no enunciado. Perceba que, segundo ele, existe um antinó em e um nó vizinho em (antinó= ventre = ponto correspondente a um mínimo) . Como um nó e um antinó estão distanciados em , então:
Beleza! Com isso, finalmente, a gente consegue encontrar o valor de :
Logo:
Passo 3
Perfeito! Agora é só usarmos esses valores encontrados no passo anterior pra determinar a equação da onda, que fica assim:
Agora, podemos responder às alternativas seguintes.
Passo 4
(a)Para saber o deslocamento em quando , é só substituir esses valores na equação da onda que a gente achou:
Passo 5
(b)Substituindo e , temos:
Passo 6
(c)Pra encontrar a velocidade, é só a gente derivar a equação da posição com relação ao tempo:
Logo:
Substituindo acima, a gente encontra isso:
Passo 7
(d)Fazendo a mesma coisa pra encontrar a velocidade em , temos:
Passo 8
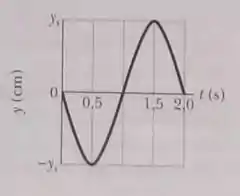
(e) Aqui, vamos plotar a função que encontramos antes em um instante fixo, com variável. Precisamos então expressar o gráfico da equação abaixo:
A equação acima representa função de período igual a e amplitude . Desenhando o comportamento dessa função, encontramos um gráfico assim:
