Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 26
Na figura, qual é o menor valor do módulo da força horizontal constante aplicada horizontalmente ao eixo da roda que permite à roda ultrapassar um degrau de altura ? O raio da roda é e a massa é .
Passo 1
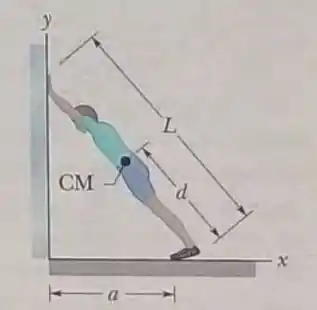
Primeiro, vamos identificar as forças atuantes, como representamos nesta figura:
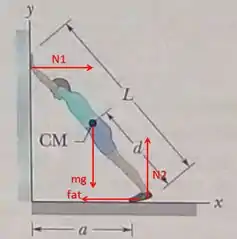
Passo 2
Do equilíbrio horizontal:
Na vertical:
Dessas duas equações, podemos concluir que:
Passo 3
Agora, vamos usar o famoso equilíbrio de torques com relação ao pé do indivíduo:
tal que é o ângulo que o corpo dele faz com o chão.
Passo 4
A figura do enunciado nos permite ver que:
“Jogando” esse valor na equação e utilizando-a na expressão , temos:
“Cortando” dos dois lados, temos:
Resposta
Exercícios de Livros Relacionados
Um lápis sextavado é colocado sobre um caderno (Figura 12-53). Determine o menor coeficiente de atrito, tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.
Um a caixa de 8,0 kg, de massa específica uniforme e duas vezes mais alta do que larga, é colocado sobre o piso de um caminhão. Qual é o maior coeficiente de atrito estático entre a caixa e o piso, ta
Um cubo está apoiado em uma parede sem atrito, formando um ângulo θ com o chão, como mostrado na Figura 12-55. Determine o menor coeficiente de atrito estático entre o cubo e o chão, necessário para e
A Figura 12-57 mostra uma escada de 20,0 kg apoiada em uma parede sem atrito e sobre uma superfície horizontal sem atrito. Para evitar que a escada escorregue, sua base é amarrada à parede com um aram
Uma escada homogênea está apoiada contra uma parede vertical sem atrito. O coeficiente de atrito estático entre a escada e o piso é 0,30 . Qual é o menor ângulo entre a escada e a horizontal para que