Exercícios de Ondas Estacionárias - Lista de Exercícios Resolvida
Questão 1
Para um fio com m de comprimento, de massa e uma tensão de , determine, para as ondas estacionárias formadas:
- A menor frequência
- A segunda menor frequência mais baixa
- A terceira menor frequência .
Questão 2
Considere uma corda feita de um material homogêneo. Qual das afirmativas a seguir está INCORRETA?
- Uma onda refletida em uma extremidade tem sempre uma frequência idêntica à onda incidente.
- A soma de uma onda totalmente refletida por uma extremidade e da onda incidente formará sempre uma onda estacionária
- Duas condições de contorno são suficientes para que o número de onda seja quantificado.
- Há propagação de energia ou de momento numa onda estacionária.
- Uma quantificação do número de onda implica numa quantificação da frequência angular.
Questão 3
A taxa de transferência de energia por uma onda ao longo de uma corda (a potência instantânea) é dada por:
Onde é a tensão.
- Usando a expressão (1), obtenha para uma onda estacionária dada por:
- Calcule a potência média por período transportada pela onda para todo o
- Para uma onda estacionária dada pela expressão (2), faça gráficos de e do deslocamento em função de para: , , , e .
- Qual o valor da potência instantânea nos nós e nos ventres da onda?
Questão 4
Quando uma massa é amarrada à extremidade de um barbante longo e fino, suspenso pelo teto, a frequência do segundo harmônico do barbante é . Acrescentando-se uma carga adicional de à massa pendurada, a frequência do segundo harmônico aumenta para . Qual é o valor de ?
Ver solução completaQuestão 5
Enquanto a corda de uma guitarra está vibrando, você toca levemente em um ponto que se situa na metade da corda para garantir que a corda não vibra naquele ponto. Que modos normais NÃO podem estar presentes na corda enquanto você a segura assim?
- Todos os modos vão estar presentes.
- Todos os modos com número par de nodos.
- Todos os modos com número ímpar de nodos.
- Somente o modo fundamental pois tem nodo no centro
- Somente o terceiro modo pois não tem nodo no centro.
Questão 6
Uma corda submetida a uma tensão de e fixa nas duas extremidades, oscila num padrão de onda estacionária correspondente ao terceiro modo normal de vibração. Uma das extremidades da corda encontra-se em e o deslocamento da corda é dado por:
(Sistema Internacional de Unidades)
Determine o comprimento da corda.
Calcule a velocidade das ondas na corda e a massa total da corda.
Obtenha a expressão da velocidade transversal das partículas da corda em função de e . Calcule essas velocidades em , nas posições .
Faça um desenho da corda em , indicando as posições dos nós e colocando os vetores velocidade nas posições e.
Desenhe a corda depois de decorrido um quarto de período .
Ver solução completaQuestão 7
Uma corda de nylon de uma guitarra tem uma densidade linear de e está sob tensão . Os suportes fixos distam . A corda vibra no trem de onda estacionário visto na figura a seguir.
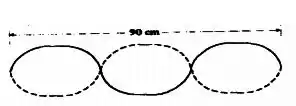
Calcule:
A velocidade
O comprimento de onda
A frequência das ondas componentes cuja superposição causa esta vibração
Ver solução completaQuestão 8
Uma corda com cm de comprimento tem uma massa de g e um tensão de .
- Qual é a velocidade de uma onda nesta corda?
- Qual é a frequência de ressonância mais baixa desta corda?
Questão 9
A função de onda para uma onda progressiva em uma corda esticada é ( em unidades do SI):
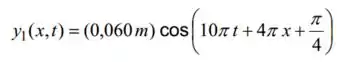
Suponha que a corda possui uma massa por unidade de comprimento de
- Obtenha o comprimento de onda, a velocidade e o sentido de propagação da onda.
- Obtenha o valor máximo de velocidade transversal da corda. Para a posição , em que instantes esse valor máximo ocorre?( Dê os dois primeiros, para
- Determine a tensão na corda e a potência média transmitida por esta onda.
- Escreva a função de onda que sobreposta a uma função produza uma onda estacionária. Obtenha a função de onda estacionária.
- Determine as duas primeiras posições para os dois primeiros nós da onda estacionária gerada.
Questão 10
Uma corda submetida a uma tensão de e fixa nas duas extremidades, oscila num padrão de onda estacionária correspondente ao terceiro modo normal de vibração. Uma das extremidades da corda encontra-se em e o deslocamento da corda é dado por:
(Sistema Internacional de Unidades)
Determine o comprimento da corda.
Calcule a velocidade das ondas na corda e a massa total da corda.
Obtenha a expressão da velocidade transversal das partículas da corda em função de e . Calcule essas velocidades em , nas posições .
Faça um desenho da corda em , indicando as posições dos nós e colocando os vetores velocidade nas posições e.
Desenhe a corda depois de decorrido um quarto de período .
Ver solução completaQuestão 11
Uma onda estacionária é produzida sobre uma corda pela superposição de duas ondas transversais progressivas dadas por:
Onde e são dados em metros e em segundos.
- Considere que a corda está submetida a uma tensão de . Encontre a massa por unidade de comprimento da corda.
- Encontre a expressão da onda resultante ( como produto de duas funções, uma apenas de e outra apenas de
- Encontre o menor valor positivo de que corresponde a um nó.
- Considerando o intervalo , encontre os instantes em que a velocidade transversal dos elementos da corda são nulos.
- Desenhe a corda nos instantes do item d), no intervalo , indicando, claramente as distâncias relevantes.
Questão 12
Uma corda homogênea e inextensível de comprimento e densidade linear de massa é tensionada por um bloco de massa , como mostrado na figura. A extremidade esquerda da corda está ligada a um anel de massa desprezível, o qual pode deslizar sem atrito em uma haste vertical. Considere o eixo apontado para direita com origem na posição do anel e suponha que ondas transversais sejam produzidas na corda usando-se uma fonte externa de frequência variável (não indicada na figura). Suponha conhecida a velocidade da onda nesta corda sob estas condições e que a corda não descole da roldana em nenhum momento.
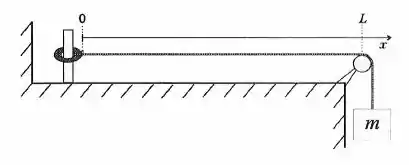
- Mostre que , onde , e são constantes, é solução da equação de ondas unidimensional (não é necessário deduzi-la) e determine a relação entre , e .
- Utilizando as condições de contorno e determine o comprimento de onda do n-ésimo modo normal de vibração.
- Esboce os três modos normais de vibração de menor frequência observados na corda.
- Calcule a frequência e o comprimento de onda do modo normal de vibração de menor frequência observado na corda se o anel é mantido fixo à haste.
Questão 13
A figura abaixo representa o perfil de uma corda vibrante de de comprimento em instantes de tempo diferentes. Considere que a corda satisfaz a equação de corda vibrante, onde o deslocamento transversal é dado como função da posição e do tempo
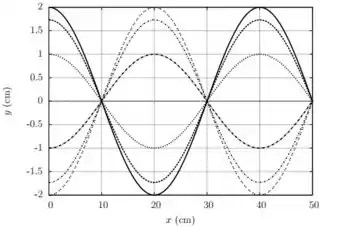
- Sabendo que o deslocamento nunca ultrapassa , determine os parâmetros , o comprimento de onda a partir do gráfico acima.
- A partir da equação de onda e sabendo que a frequência angular de vibração é , encontre a velocidade de propagação das ondas na corda.
- Que condições de contorno pra e podem gerar esta onda como um modo normal de vibração? O que pode ser dito sobre as extremidades da corda neste caso?
- Quais os outros valores do comprimento de onda que geram modos normais satisfazendo essas condições? Explique seu raciocínio.
Questão 14
Ondas estacionárias são produzidas pela interferência de duas ondas progressivas senoidais cuja frequência é . Se a distância entre o segundo nó e o quinto nó é , o comprimento de onda das ondas progressivas é
A)
B)
C)
D)
E)
Ver solução completaQuestão 15
Uma corda de de comprimento está vibrando sob uma tensão de . Os resultados de cinco fotografias estroboscópicas sucessivas são mostrados na figura abaixo. A taxa do estroboscópico é fixada em 5000 flashes por minuto, e observações revelam que o deslocamento máximo ocorreu, em relação à posição de equilíbrio da corda, nos flashes 1 e 5, sem nenhum outro máximo no intervalo entre eles. Qual a massa da corda?
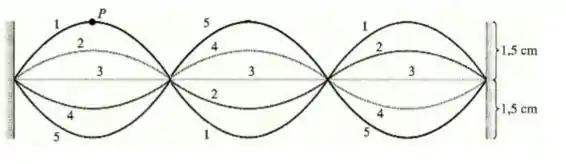
Ver solução completa
Questão 16
Uma corda fixa nas duas extremidades e submetida a uma tensão oscila em seu terceiro modo normal, com comprimento de onda e . Se a tensão for quadruplicada, os novos e para este modo serão, respectivamente:
a): e .
b): e .
c): e .
d): e .
e) e .
Ver solução completaQuestão 17
Uma onda estacionaria estabelecida em uma corda infinita apresenta espaçamento entre nós consecutivos. Se a força de tração for dobrada, mas a frequência mantida fixa, qual será o espaçamento entre nós consecutivos?
- , ou seja, não haverá mudança.
Questão 18
Uma onda estacionária de amplitude , com dois nós intermediários e frequência se formou numa corda de comprimento fixa nas duas extremidades. A função de onda que a descreve corretamente é a:
Questão 19
Considere a onda . A superposição com qual das ondas a seguir produz uma onda estacionária?
Questão 20
Uma onda estacionária numa corda está oscilando com frequência de 500 Hz, como mostra a figura. A densidade linear de massa da corda é 10,0g/m. Qual é a tensão na corda?
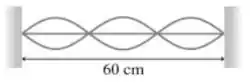
Questão 21
Uma corda presa a um oscilador senoidal no ponto e apoiada em um suporte no ponto (vide figura), é tensionada por um bloco de massa . A distância entre e é , a massa específica linear da corda é e a frequência do oscilador é . A amplitude de deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto .
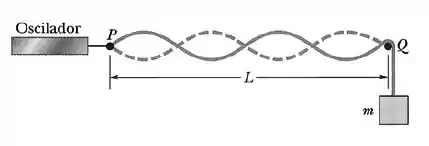
- Qual deve ser o valor da massa para que o oscilador produza na corda o quarto harmônico?
- Se , qual é a frequência do quarto harmônico?
Se necessário, use .
Ver solução completaQuestão 22
Uma ponta de uma corda é ligada a um vibrador mecânico de pequenas amplitudes de . A corda passa por uma polia a uma distância da ponta do vibrador e é esticada por um bloco de massa variável .A amplitude do movimento na ponta do oscilador é suficientemente pequena para que este ponto seja considerado um nó. Também deve se formar um nó no ponto em que a corda toca a roldana. Observa-se que dois possíveis valores da massa que geram ondas estacionárias nas cordas são e , e que nenhum valor de massa intermediário entre estes dois valores gera ondas estacionárias.
- Calcule a densidade linear da corda.
- Para que valor de será gerada a frequência fundamental da corda?
- Se fixarmos e variarmos o comprimento de entre e , quantas configurações diferentes de ondas estacionárias observaremos? Despreze a variação da densidade linear com o comprimento da corda.
Questão 23
Uma corda de de comprimento tem densidade linear de massa igual a .
- Qual deve ser a tensão da corda se seu segundo harmônico tiver a mesma frequência que o segundo modo de ressonância de um tubo de de comprimento aberto em apenas uma extremidade?
- Considere a corda estiver vibrando em um modo estacionário descrito pela equação,
Sendo dado em metros e em segundos. Quantos antinodos podem ser observados na corda?
Dado:
Ver solução completaQuestão 24
Duas ondas em uma corda infinita são representadas pelas funções:
E e estão em metros, t em segundos. Qual é, em metros, a posição do primeiro nó da onda estacionária resultante?
Dado:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Ver solução completaQuestão 25
Uma onda estacionária estabelecida em uma corda infinita apresenta espaçamento entre nós consecutivos. Se a força de tração é dobrada, mas a frequência mantida fixa, qual será o espaçamento entre nós consecutivos?
(a)
(b)
(c)
(d)
(e) , ou seja, não haverá mudança.
Ver solução completaQuestão 26
Uma corda de piano tem comprimento L e massa M. Se a frequência fundamental é f, a força de tração na corda é:
a) 4LM;
b) 2Lf/m;
c) 4MLf;
d) 2M/L;
e) 4/M;
Ver solução completaQuestão 27
Dadas as seguintes funções: Quais delas representam ondas propagantes ou progressivas?
- Somente .
- e .
- Somente .
- Somente .
- , , e .
Questão 28
Uma corda de comprimento presa nas extremidades e , submetida a uma tensão de , oscila no terceiro harmônico de uma onda estacionária. O deslocamento transversal da corda é dada por:
Onde e são dados em metros e em segundos.
- Qual é o comprimento da corda?
- Qual é a massa da corda?
- Calcule a velocidade transversal máxima de um ponto situado sobre o ventre de uma corda.
- Se a corda oscilar no quinto harmônico, qual será o período de oscilação?
Questão 29
Uma corda com as duas extremidades fixas vibra no modo vibracional do primeiro harmônico de acordo com a seguinte equação: onde o valor de é dado em metros.
- Escreva expressões para as funções e das ondas que viajam simultaneamente na corda (para a direita e para a esquerda, respectivamente), ambas com a mesma amplitude e que fornecem o resultado da onda estacionária acima. Calcule o valor de .
- Qual a velocidade das ondas componentes e ?
- Qual é o comprimento da corda e qual é a distância entre dois nós na onda dada por acima?
- Qual é a maior velocidade transversal de uma partícula na corda e qual é a posição mais próxima da extremidade esquerda fixa, considerada , onde esta velocidade máxima ocorre?
- Se a corda passar a vibrar no segundo harmônico, qual será o novo comprimento de onda e a nova frequência de vibração?
Questão 30
Uma corda está esticada e vibra com o padrão mostrado na figura. Se o seu comprimento natural é de e a tração do fio e a sua densidade linear , é correta a opção para o comprimento de onda λ e frequência :
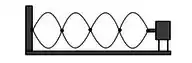
- ;
- ;
- ;
- ;
Questão 31
Uma corda de densidade linear de massa é esticada sob uma tensão de . A corda tem de comprimento e, simultaneamente, a partir de cada uma das extremidades, introduzem-se oscilações harmônicas de frequências iguais , de mesma amplitude e de fases opostas.
Dados:
a) Depois de quantos segundos as frentes de onda se encontram?
b) Escreva a equação da onda
c) Escreva a equação para a elongação para um ponto no meio do fio.
d) Considerando um tempo suficientemente longo, comparado com o tempo para a onda percorrer toda a corda, quantos nós terá a onda estacionária?
Ver solução completaQuestão 32
Uma corda de violino de comprimento de vibra no seu terceiro harmônico com uma frequência de Quantos nodos, além das extremidades fixas da corda, possui esta onda estacionária e qual o seu comprimento de onda?
nodos,
nodos,
nodos,
nodos,
nodo,
Ver solução completaQuestão 33
Uma corda presa a um oscilador senoidal no ponto e apoiada em um suporte no ponto (vide figura), é tensionada por um bloco. A distância entre e é e a frequência do oscilador é . A amplitude de deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto . Uma onda estacionária aparece quando a massa do bloco é ou , mas não aparece para nenhuma massa entre esses dois valores.
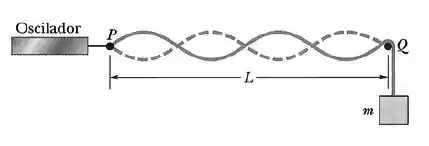
- Qual é o comprimento da onda na corda quando a massa do bloco é ? E quando é ?
- Qual é a massa específica linear da corda?
Se necessário, use .
Ver solução completaQuestão 34
I-Num violino a parte vibrante das cordas, entre os pontos fixos A e B (ver figura), tem de comprimento. Considere que a corda com densidade linear de massa de emite uma nota Sol () quando tocada sem que se coloque o dedo nela.

- Calcule a tensão na corda, considerando que as cordas vibram no harmônicofundamental.
- Determine onde se deve colocar o dedo pressionando a corda, com respeito ao ponto B, para que a corda passe a emitir uma nota Ré () como frequência fundamental? Suponha que a tensão não muda.
Questão 35
I-Uma onda estacionária transversal em uma corda longa possui um antinó em e um nó vizinho em A figura ao lado mostra o deslocamento da partícula da corda situada em .
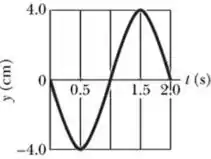
- Obtenha o comprimento de onda, o período e a máxima amplitude das oscilações na corda.
- Escreva a função representada no gráfico, especificando valores numéricos das constantes e suas unidades.
- Obtenha a função que representa a onda (vibração) estacionária (especificando valores numéricos das constantes e suas unidades).
- Faça o desenho da corda no instante no intervalo de a
- Obtenha a função que descreve a velocidade transversal das partículas da corda e calcule a velocidade da partícula situada em no instante
Questão 36
Marque a alternativa INCORRETA:
- Uma onda estacionária pode ser descrita como a combinação de duas ondas progressivas de mesma frequência e sentidos opostos se propagando com a mesma velocidade.
- A combinação de duas ondas harmônicas progressivas de mesmo sentido e freqüências ligeiramente diferentes, se propagando com a mesma velocidade, resulta em uma onda progressiva com amplitude variável.
- A amplitude de onda resultante da interferência de duas ondas progressivas depende da diferença de fase entre as duas.
- A amplitude da onda resultante da interferência de duas ondas progressivas depende da amplitude de cada uma.
- A amplitude da onda resultante da interferência de duas ondas progressivas com sentidos opostos é sempre zero.
Questão 37
. Um gerador de frequências está acoplado a uma mola, cuja constante de rigidez é presa a um bloco de massa . Os sistema massa-mola por sua vez está preso a direita a uma corda de comprimento e massa . Para que o bloco não se desloque para direita uma outra corda é presa a ele pela esquerda (ver figura) e verifica-se que a tensão sobre ela é de .
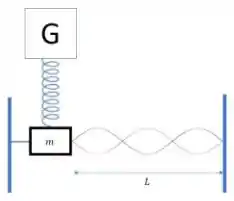
Considere que o amortecimento seja fraco e que depois de um certo tempo que o gerador de frequências está ligado se atinja o estado estacionário e a corda a direita esteja no terceiro modo de vibração cuja amplitude de deslocamento seja . A amplitude de oscilação do bloco é bem menor e o ponto de contato da corda com o bloco pode ser considerado um nó.
Com base nessas informações:
Determine o comprimento de onda da onda estacionária da corda a direita.
Determine a frequência de oscilação da corda e a do gerador de frequências.
Escreva a equação da onda estacionária da corda, dado que no instante os deslocamentos dos pontos da corda eram máximos. Não substitua o valor numérico de caso apareça.
Ver solução completaQuestão 38
Quando uma corda está vibrando em um padrão de onda estacionária, a potência transmitida na direção do comprimento da corda através de um antinodo, comparada à potência transmitida através de um nodo, é:
A) maior
B) menor
C) a mesma (zero)
D) a mesma (diferente de zero)
E) às vezes é maior, às vezes é menor, e às vezes é a mesma
Ver solução completaQuestão 39
Marque a alternativa Errada:
a) Quando fazemos a corda de um violão soar, formam-se ondas estacionárias e escutamos as frequências de ressonância da corda.
b) Se quadruplicarmos a tensão de uma corda cujas extremidades estão fixas, a frequência de ressonância fundamental dobrará..
c) Enquanto uma onda progressiva se propaga em uma corda esticada, a quantidade de energia em cada pedaço da corda não é constante, pois a energia é transportada pela onda.
d) A velocidade de propagação de uma onda harmônica em uma corda cresce linearmente quando aumentamos a frequência da onda.
e) As velocidades máximas das partículas de uma corda oscilante dependem da amplitude e da frequência da oscilação.
Ver solução completaQuestão 40
A figura mostra ondas estacionárias em uma corda vibrando com frequência de . Ela tem de comprimento, densidade linear de massa . As duas extremidades estão fixas. Analise as afirmações abaixo.

(I)Todos os pontos da corda vibram com a mesma amplitude.
(II)Todos os pontos da corda vibram com a mesma freqüência.
(III)O comprimento de onda na corda é de .
(IV)A velocidade de propagação da onda na corda é de .
(V) A força tensora na corda é de , aproximadamente.
Assinale a alternativa correta:
- Somente I e III são falsas.
- Somente I e II são falsas.
- Somente I e II são verdadeiras.
- Somente II e IV são verdadeiras.
- I, II e V são falsas.
Questão 41
Duas ondas, e , propagam em uma corda infinitamente longa. As ondas são descritas por
onde , e estão em metros e está em segundos.
Determine o comprimento de onda , o período , o módulo da velocidade e o sentido do movimento de cada uma das duas ondas.
Seja . A onda descrita por propaga? Se SIM, com que velocidade e em que sentido? Se NÃO, descreva o que ocorre com a corda.
Esboce os gráficos de , e de , no intervalo .
Determine a velocidade de um ponto da corda na posição e no instante .
Dado: .
Ver solução completaQuestão 42
Na figura abaixo a extremidade de uma corda é presa a um oscilador senoidal de frequência e a outra é presa a uma massa , passando por uma roldana. A massa específica da corda é e a amplitude do oscilador é suficientemente pequena para que o ponto possa ser considerado um nó.
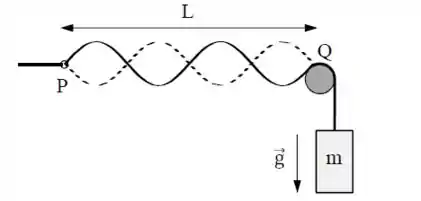
a) Qual deve ser a massa para que o oscilador produza uma oscilação no harmônico da corda? Expresse sua resposta em termos de
b) Nas condições do item (a) determine a ordem do harmônico se dobrarmos o comprimento da corda, mantendo tudo o mais inalterado.
Ver solução completaQuestão 43
Uma corda com as extremidades fixas, sujeita a uma tensão de , oscila no quarto harmônico de uma onda estacionária. O deslocamento da corda é dado por, , onde em uma das extremidades da corda, x está em metros e t está em segundos.
Determine:
- O comprimento da corda
- A amplitude e a velocidade das ondas na corda (iguais, exceto pelo sentido de propagação) cuja superposição produz esta oscilação.
- A massa da corda
- A posição dos dois primeiros anti-nós (ventres)
- A velocidade transversal de uma partícula da corda no ponto para
- Se a corda oscilasse no terceiro harmônico, qual seria o período de oscilação
Questão 44
Uma corda de violino com 30 cm de comprimento vibra no seu segundo modo normal de vibração quando é colocada próxima a uma fonte sonora que emite um som com frequência igual a 440 Hz. Suponha que a corda do violino em repouso coincide com o eixo Ox.
(a) Qual a frequência da onda estacionária observada? Justifique a sua resposta.
(b) Determine a partir da expressão geral da onda estacionária
o comprimento de onda das ondas progressivas que produziram a onda estacionária observada.
(c) Determine a velocidade v da onda progressiva que produziu a onda estacionária observada.
(d) Determine a localização ao longo do eixo Ox dos pontos da corda onde estão os ventres ou antinós.
(e) Sabendo que o movimento de um ponto da corda que dista 7,5 cm da extremidade direita da corda do violino (origem do eixo Ox) é dada por , obtenha a função que descreve a onda estacionária na corda.
Ver solução completaQuestão 45
A figura mostra um fio composto de dois pedaços emendados de fios de um material 1 e de um material 2 de mesma área de seção transversal com densidades volumétricas , no caso do material 1 e para o material 2. Sabe-se que o fio do material 1 tem de comprimento, que na extremidade do fio do material 2 está pendurado um bloco com de massa e que a distância entre a junção dos fios e a roldana de suporte é . Ao usar um gerador de ondas externo de frequência ajustável para criar ondas transversais no fio composto, determine (assuma que tanto a extremidade esquerda do fio ligada ao gerador quanto aquela em contato com a roldana são nós):
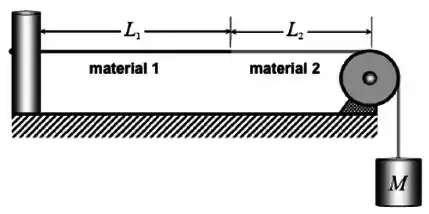
Dica: para simplificar suas contas, use como valor para a aceleração da gravidade .
(a) a velocidade de propagação v das ondas progressivas em cada pedaço do fio composto;
(b) a ordem dos harmônicos mais baixos que aparecem na corda quando a frequência f da fonte é ajustada de modo a originar uma onda estacionária com nó exatamente na junção dos fios;
(c) a frequência f do gerador externo correspondente à onda estacionária do ítem anterior.
(d) os comprimentos de onda e em cada fio na configuração do item (b).
Ver solução completaQuestão 46
Uma corda de de comprimento tem densidade linear de massa igual a .
- Qual deve ser a tensão da corda se seu segundo harmônico tiver a mesma frequência que o segundo modo de ressonância de um tubo de de comprimento aberto em apenas uma extremidade?
- Considere a corda estiver vibrando em um modo estacionário descrito pela equação,
Sendo dado em metros e em segundos. Quantos antinodos podem ser observados na corda?
Dado:
Ver solução completaQuestão 47
Uma corda de um violino pode ser representada por uma corda presa nas duas extremidades de densidade linear e comprimento L. A velocidade de propagação de ondas transversais nessa corda é v.
(a) Encontre as frequências e os comprimentos de onda dos modos normais de vibração dessa corda do violino.
(b) Desenhe a forma da corda associada aos três modos de vibração mais baixos
(c) Mostre que os modos normais de vibração são descritos pela equação:
(d) Sabendo que um elemento da corda se move segundo um movimento harmônico simples, calcule a energia total de oscilação da corda, quando está vibrando no n-ésimo modo normal.
Ver solução completaQuestão 48
Em um laboratório, um estudante de engenharia é capaz de gerar três tipos de ondas em uma corda:
a) Considerando que o estudante gera apenas as ondas y1 e y2 na corda, responda às perguntas abaixo.
(i) Qual é a amplitude da onda resultante. Demonstre sua resposta.
(ii) A onda resultante na corda é uma onda estacionária? Justifique sua resposta.
(iii) A potência que a onda resultante transmite é maior, menor ou igual à potência transmitida pela onda y1? Justifique sua resposta.
b) Agora, considere que a corda tem suas extremidades fixadas em x = 0 e x = L. O estudante gera apenas as ondas y1 e y3 e observa que uma onda estacionária de 4 ventres (quarto harmônico) é gerada na corda. Escreva a expressão matemática da onda resultante na forma e determine as constates A; a; b; c e d apenas em termos de ym, ω e L.
Ver solução completaQuestão 49
Marcelo e Edivaldo seguram pelas extremidades uma corda de comprimento L e densidade linear , aplicando uma tensão T. Ao movimentar as extremidades, eles geram ondas harmônicas progressivas em cada extremidade, de forma a obter ao final uma onda estacionária na corda, com os ventres nas posições de Marcelo () e Edivaldo ().
a) Quais as condições de contorno a serem satisfeitas pela onda estacionária formada?
b) Marcelo e Edivaldo movimentam suas extremidades em oposição de fase deslocando-as entre A e -A, de forma a excitar o modo fundamental de oscilação. Qual a função de onda progressiva gerada por Marcelo () e Edivaldo (), se no instante inicial (t = 0) estão segurando a corda nas posições ?
c) Qual a expressão da onda estacionária formada, em função de x e t?
d) Se eles passarem a movimentar a corda em fase, qual a frequência de oscilação mínima excitada? Justifique a resposta.
Ver solução completaQuestão 50
Uma corda com um vibrador de freqüência fixa em uma extremidade é submetida a tensões variáveis. A corda é fixa nas duas extremidades. Quando a tensão é 20 N, verifica-se uma ressonância com 3 anti-nodos. Que tensão causaria uma ressonância com 2 anti-nós nesta corda?
A) 30 N
B) 45 N
C) 80 N
D) 8,9 N
E) 13 N
Ver solução completaQuestão 51
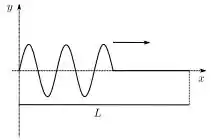
Uma pessoa segura uma ponta de um pedaço de corda de tal modo que a outra extremidade não está em contato com o chão. Esta pessoa mexe sua mão na horizontal de tal modo que o movimento da extremidade da corda em contato com a sua mão pode ser aproximado ao movimento horizontal de um oscilador harmônico simples.
Depois de um tempo longo em comparação ao tempo necessário para que uma onda progressiva percorra um comprimento de onda, qual(quais) da(s) afirmação(ões) seguinte(s) é (são) verdadeira(s):
-O movimento da corda corresponde a uma onda progressiva se propagando de cima pra baixo.
-A onda criada pelo movimento de mão não é refletida porque a extremidade inferior da corda está solta.
-O movimento da corda é composto por uma onda subindo e uma descendo.
São verdadeiras:
- e
- e
- Todas
- Nenhuma
Questão 52
Uma corda de é fixada nas duas extremidades e esticada até a velocidade da onda ser de . Qual é a frequência da onda estacionária, em Hz, mostrada na figura abaixo?
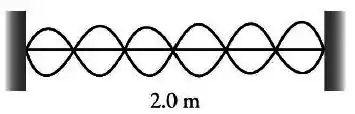
- 230
- 350
- 120
- 470
- 140
Questão 53
Se duas ondas progressivas dadas por e se combinam para formar uma onda estacionária em uma corda, a distância entre nós vizinhos é:
a) 2π/k;
b) π/k ;
c) k/2π;
d) vtπ;
e) 2vtπ;
Ver solução completaQuestão 54
Uma onda estacionária é visualizada num fio de comprimento L, sua frequência é f1 e ela está no 1º harmônico. Analise as seguintes proposições e marque a alternativa que contém apenas proposições verdadeiras.
I - Uma possível expressão para a forma dessa onda estacionária é dada por:
Onde A é a amplitude de oscilação, λ o comprimento de onda e ф uma constante de fase.
II - Para visualizar o 2º harmônico a frequência será f2 = 2f1;
III - Seja λ1 o comprimento de onda do 1º harmônico. O comprimento de onda λ3 do 3º harmônico é λ3 = λ1/3.
IV - A velocidade de propagação da onda no 2º harmônico é o dobro da velocidade no 1º harmônico;
V - Caso a tensão no fio seja dobrada, a frequência da onda no 1o harmônico será dada por 2f1;
VI - Caso a tensão no fio seja dobrada, a velocidade de propagação da onda no 1º harmônico será dobrada.
a) Nenhuma;
b) Todas;
c) III, IV, V;
d) II, V, VI;
e) I, III, VI;
f) I, II, IV, V;
g) I,II, III, IV;
h) I, IIe III.
Ver solução completaQuestão 55
Duas cordas e possuem o mesmo comprimento e a mesma densidade linear, mas a corda está submetida a uma tensão maior que acorda . A figura abaixo mostra quatro situações, de a , nas quais existem ondas estacionárias nas duas cordas.
Em que situação existe a possibilidade de que as cordas e estejam oscilando com a mesma frequência natural?
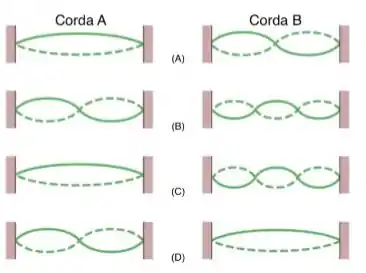
Situação .
Situação .
Situação .
Situação .
Em nenhuma das situações existe a possibilidade de que as cordas e oscilem com a mesma freqüência natural.
Ver solução completaQuestão 56
Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .
c) Após um longo intervalo de tempo a onda terá percorrido a corda várias vezes, ao se refletir nos extremos, formando uma onda estacionária. Supondo que a amplitude das oscilações em possa ser desprezada (por ser pequena em comparação com a amplitude final da onda formada), faça um esboço do perfil da corda num instante tal que . Deixe claro a localização dos nós e dos ventres.
Onde aplicável, a resposta pode ficar em função de .
Ver solução completaQuestão 57
Uma corda com de comprimento está sujeita a uma tensão de . Ela tem suas extremidade fixas e oscila em um padrão de vibrações (ondas estacionária) resultante da superposição das ondas abaixo:
sendo , e em metros e em segundos
Use o princípio de Superposição de Ondas para obter a função da onda estacionária (ou vibração estacionária) nessa corda.
A que modo normal corresponde a vibração dessa corda? Qual o número total de nós, incluindo os extremos
Desenhe o formato da corda ( versus ) para (considere as extremidade da corda em e ). Faça o mesmo para .
Determine o comprimento de onda , a frequência e a velocidade da onda , vibrando no modo fundamental.
Ver solução completaQuestão 58
Dois geradores localizados nas extremidades de uma corda muito longa, com densidade linear de massa de , produzem ondas descritas pelas funções a seguir:
- Determine o período, o comprimento de onda e a velocidade dessas duas ondas, especificando em que sentido elas se propagam.
- Obtenha a função que descreve a onda estacionária resultante da superposição dessas duas ondas.
- Determine a posição dos três primeiros nós, para valores positivos de
- Obtenha a velocidade transversal dos pontos da corda em função de e Determine a expressão para essa velocidade no primeiro instante em que todos os elementos da corda possuem deslocamento nulo.
- Calcule a potência média transmitida por cada uma das ondas e a potência média transmitida pela onda estacionária.
Questão 59
Uma corda de violão com densidade linear de , presa em ambas as extremidades, está sujeita a uma tensão de .
- Com que velocidade se propaga um pulso transversal nessa corda?
- Para um dado comprimento fixo, desenhe os três primeiros harmônicos. Para os diversos modos de vibração, escreva a relação entre e os respectivos comprimentos de onda .
- Qual deve ser o comprimento da corda para que sua frequência fundamental seja ?
- Para tocar uma nota de frequência , prende-se a corda com um dedo, de forma a utilizar apenas uma fração do seu comprimento. Qual é essa fração ?
Questão 60
O modo fundamental de vibração de uma corda de violão (fixa nas extremidades) é descrito por .
- Determine o comprimento de onda, a frequência, e a amplitude máxima de vibração.
- Determine o comprimento dessa corda.
- Faça um desenho esquemático da onda estacionária de deslocamento, para cada um dos 3 primeiros harmônicos num desses tubos, e determine a relação entre o comprimento do tubo e o comprimento de onda. A partir dessas relações, ache a expressão geral para a frequência do enésimo harmônico, em função de e .
- Determine os possíveis valores do comprimento daqueles tubos que ressoam com a frequência fundamental da corda do violão.
Perto da corda do violão que vibra no modo fundamental, encontram-se vários tubos de diferentes comprimentos, de valores entre e , abertos em ambas as extremidades. Alguns deles entram em ressonância devido ao som produzido pela corda do violão. Considere .
Questão 61
Uma corda de guitarra e fixada nas duas extremidades. Se você apertar a corda para aumentar a sua tensão
- As frequências dos modos normais irão aumentar e os comprimentos de onda associados não serão afetados.
- O comprimento de onda aumenta e a frequência dos modos normais não e alterada.
- As frequências dos modos normais irão aumentar e os comprimentos de onda associados irão diminuir.
- Ambos, comprimento de onda e frequência, irão aumentar.
- Ambos, comprimento de onda e frequência, não serão alterados.
Questão 62
Qual das afirmações abaixo é uma característica dos ventres de uma onda estacionária numa corda?
- A corda realiza oscilações longitudinais nesses pontos.
- A energia mecânica é puramente cinética nesses pontos.
- As ondas em sentidos opostos estão sempre em fase.
- As ondas em sentidos opostos estão sempre em oposição de fase.
- As ondas de mesmo sentido estão sempre em oposição de fase.
Questão 63
. Uma corda, presa em suas extremidades, está vibrando como uma onda estacionária. A onda estacionária é produzida pela superposição de duas ondas senoidais, e , que têm a mesma frequência, a mesma velocidade, e as mesmas amplitudes, mas que propagam-se ao longo da corda em sentidos opostos. A vibração da corda, no , é representada pela equação:
onde é o deslocamento transversal de um elemento qualquer da corda na posição e no
instante . Para a onda estacionária descrita pela função , podemos afirmar que a função da
componente , que se desloca no sentido positivo do eixo é dada por:
Ver solução completa
Questão 64
Uma onda estacionária em uma corda vibra como mostrado na figura. Se, nesse modo de vibração, T e L são, respetivamente, a tensão e o comprimento da corda e f é a frequência de vibração, pode-se dizer que:


a) Se , e , a corda vibra seguindo o modo mostrado na figura d.
b) Se , mantendo L e f, a corda vibra seguindo o modo mostrado na figura b.
c) Se e , mantendo f, a corda vibra seguindo o modo mostrado na figura c.
d) Se , mantendo L e f, a corda vibra seguindo o modo mostrado na figura a.
e) Nenhum dos modos de vibração mostrados nas figuras de (a) a (d) pode-se obter mudando T e/ou L e/ou f .
Ver solução completaQuestão 65
Considere as afirmações abaixo e marque verdadeiro ou falso.
a) ( ) No caso de uma onda se propagando em uma corda na direção do eixo , cada ponto da corda conserva seu deslocamento .
b) ( ) Quando uma onda se propaga ao longo de uma corda esticada, cada elemento da corda possui a energia mecânica total constante.
c) ( ) Quando duas ondas senoidais iguais se propagam em sentidos opostos, o resultado é uma interferência totalmente destrutiva.
d) ( ) A amplitude de uma onda estacionária varia com a posição .
e) ( ) A velocidade transversal de um elemento de corda oscilando transversalmente em MHS é máxima quando está passando pela posição .
Ver solução completaQuestão 66
Uma corda homogênea, de massa e comprimento , está presa em ambos os extremos e submetida a uma tensão . A corda vibra num dado modo normal. Observa-se que um certo ponto da corda leva para ir de seu deslocamento máximo positivo ao mínimo e voltar ao máximo.
Quantos ventres de oscilação estão presentes na corda?
- 3
- 1
- 2
- 4
- 6
Questão 67
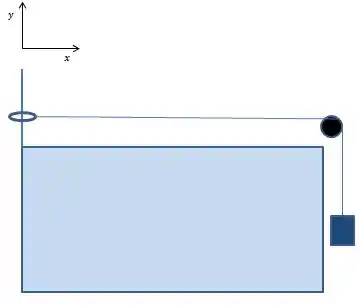
Uma corda homogênea e inextensível de comprimento e densidade linear de massa é tensionada por um bloco de massa , como mostrado na figura. A extremidade esquerda da corda está ligada a um anel de massa desprezível, o qual pode deslizar sem atrito em uma haste vertical. Considere o eixo apontado para direita com origem na posição do anel e suponha que ondas transversais sejam produzidas na corda usando-se uma fonte externa de frequência variável (não indicada na figura). Suponha conhecida a velocidade da onda nesta corda sob estas condições e que a corda não descole da roldana em nenhum momento.
- Mostre que , onde e são constantes, é solução da equação de onda unidimensional(não é necessário deduzi-la) e determine a relação entre e .
- Utilizando as condições de contorno e determine o comprimento de onda do n-ésimo modo normal de vibração.
- Esboce os três modos normais de vibração de menor frequência observados na corda indicando explicitamente o comprimento de onda de cada um.
Questão 68
Marque a opção que indica quais das afirmativas abaixo estão INCORRETAS:
- A soma de duas ondas estacionárias quaisquer também apresenta nós permanentes.
- Um pulso em uma corda é invertido ao ser refletido em uma extremidade fixa.
- A velocidade de propagação de uma onda mecânica depende da intensidade da força restauradora sobre as partículas do meio.
- Somente I.
- Somente II.
- Somente III.
- Somente I e II.
- Somente II e III.
- Somente I e III.
- Todas estão corretas.
- Nenhuma está correta.
Questão 69
(Capítulo 15.Exercícios – Exercício 15) Uma das extremidades de um fio é presa a um dos ramos de um diapasão eletricamente excitado com uma frequência igual a . A outra extremidade passa sobre uma polia e suporta um objeto com massa igual a . A densidade linear do fio é igual a . a) Qual é a velocidade de propagação de uma onda transversal na corda? b) Qual é o comprimento de onda? c) Como suas respostas dos itens (a) e (b) se modificam se a massa do objeto aumentar para ?
Ver solução completaQuestão 70
(Capítulo 15.Exercícios – Exercícios 33) As ondas estacionárias em um fio são descritas pela Equação (15.28), com , e . A extremidade esquerda do fio está no ponto . Calcule as distâncias entre a extremidade esquerda do fio e a) os nós da onda estacionária, b) os ventres da onda estacionária.
Ver solução completaQuestão 71
(Capítulo 15.Exercícios – Exercícios 13) Uma onda transversal em uma corda possui amplitude de , comprimento de onda igual a e velocidade de . Ela é representada pela função dada no exercício 15.12. a) Para o tempo , calcule para intervalos de iguais a (ou seja, e assim por diante) desde até . Faça um gráfico dos resultados obtidos. Essa é a forma da corda para o tempo . b) Repita o cálculo para os mesmos intervalos de para o tempo e para o tempo . Faça um gráfico da forma da corda para esses tempos. Qual é o sentido de propagação da corda?
Ver solução completaQuestão 72
No arranjo mostrado na figura, uma massa está pendurada em uma das extremidades de uma corda, de densidade linear de massa igual a , e que passa sobre uma polia leve. Na outra extremidade da corda, um oscilador senoidal coloca a corda em movimento com uma frequência constante de . Observa-se que os elementos da corda situados nos pontos e estão aproximadamente em repouso, com deslocamento quase nulo durante o movimento de vibração da corda, de modo que eles podem ser considerados como nós.
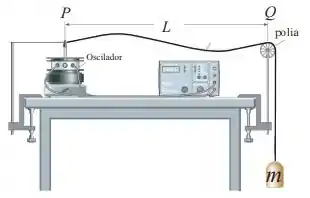
Podemos afirmar que o -ésimo modo normal que se estabelece na corda quando a distância entre os pontos e é é: (Use )
a) .
b) .
c) .
d)
e) .
f) .
g) nenhuma das respostas indicadas.
Ver solução completaQuestão 73
Quando uma raquete de tênis acerta uma bola, ela começa a vibrar. As vibrações têm frequências bem definidas, que dependem do tamanho da raquete e do padrão de vibração. Considere uma raquete, representada na figura ao lado, vibrando no padrão com uma frequência de .
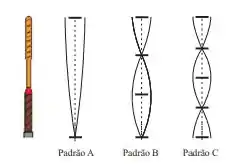
Podemos afirmar que nos padrões e ela vibrará com as seguintes frequências, respectivamente:
a) e .
b) e .
c) e .
d) e .
e) e .
f) e .
g) nenhuma das respostas indicadas.
Ver solução completaQuestão 74
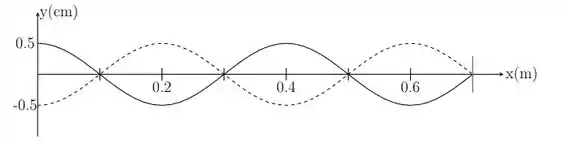
Uma corda fixa em um dos extremos e livres para oscilar no outro, vibra num dado modo normal. A velocidade de propagação das ondas nesta corda vale . A figura mostra o perfil da corda num dado instante em que todos os deslocamentos são máximos.
- Determine o comprimento de onda e a frequência de oscilação da corda neste modo normal.
- Determine o comprimento de onda e a frequência de oscilação para o modo normal de maior frequência logo abaixo deste.
- Determine as posições dos nós no modo do item .
- Escreva a equação da onda estacionária que descreve a oscilação da corda para este novo modo normal. (Suponha a mesma amplitude do modo dado no enunciado e que os deslocamentos são máximos em ).
Questão 75
Uma onda estacionária transversal produzida numa corda de comprimento infinito tem as seguintes características: o deslocamento de um ponto da corda em em função do tempo está descrito na figura ao lado e, além disso, o ponto é um ventre e o primeiro nó da onda se localiza em .
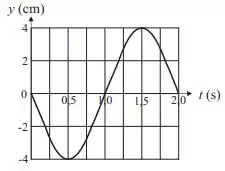
Determine a função que descreve o deslocamento da corda em função do tempo, com todos os valores numéricos pertinentes.
Ver solução completaQuestão 76
Enquanto a corda de uma guitarra esta vibrando, você toca levemente em um ponto que se situa na metade da corda para garantir que a corda não vibra naquele ponto. Que modos normais NÃO podem estar presentes na corda enquanto você a segura assim?
- Todos os modos vão estar presentes.
- Todos os modos com um número par de nodos.
- Todos os modos com um número ímpar de nodos.
- Somente o modo fundamental, pois tem nodo no centro.
- Somente o terceiro, pois não tem um nodo no centro.
Questão 77
Uma onda estacionária está oscilando com uma frequência de 690 Hz em uma corda presa nas duas extremidades, como mostrado na figura abaixo. A velocidade das ondas que formam o padrão estacionário observado nessa corda é mais próxima de
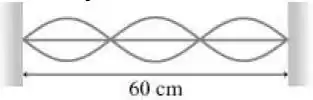
A) 140 m/s
B) 410 m/s
C) 210 m/s
D) 280 m/s
E) 70 m/s
Ver solução completaQuestão 78
Numa experiência de laboratório, ondas de 120 Hz são excitadas numa corda com densidade linear igual a 0,5 g/m conforme a figura. O copo preso na extremidade da corda tem massa igual a 50 g e contém, inicialmente, 250 g de água.
Observa-se que o copo está furado e que a água vai escoando lentamente. Suponha que o comprimento da corda seja mantido fixo (L = 0,5 m)
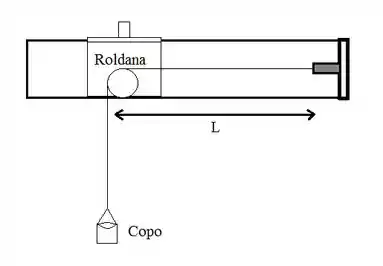
a) Calcule as massas de água no copo para as quais serão observadas ressonância na corda.
b) Desenhe a onda estacionária na corda para a primeira ressonância a ser observada.
Ver solução completaQuestão 79
. Um corpo está pendurado em equilíbrio em uma corda com um comprimento total e uma densidade de massa linear de . A corda passa em torno de duas polias leves sem atrito que são separadas por uma distância (Veja a figura abaixo). Suponha que a tensão na corda é de . Em que frequência deve vibrar a corda entre as polias a fim de formar o padrão de onda estacionária mostrado na figura ?
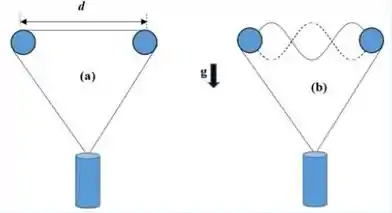
.
.
.
.
.
Ver solução completaQuestão 80
Ondas estacionárias são produzidas pela interferência de duas ondas progressivas senoidais, cada uma com frequência . A distância do segundo nodo para o quinto nodo e de . O comprimento de onda e a velocidade das duas ondas originais são respectivamente:
Questão 81
Uma corda oscila no terceiro harmônico, de acordo com a equação . Quais são, respectivamente, o comprimento da corda e a velocidade transversal de uma partícula da corda no ponto para ?
Ver solução completaQuestão 82
Uma corda de violino de de comprimento, com massa específica linear de , é colocada perto de um alto-falante alimentado por um oscilador de áudio de frequência variável. Quando a frequência do oscilador varia no intervalo de a , observa-se que a corda entra em oscilação apenas nas frequências de e .
- Desenhe o padrão de onda estacionária na corda nos dois casos.
- Determine a tração na corda.
Questão 83
O movimento de uma partícula, descrito pela função , é mostrado no gráfico abaixo.
Dele deduzimos que:
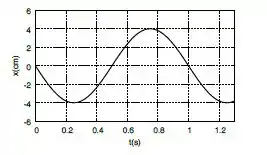
- e
Questão 84
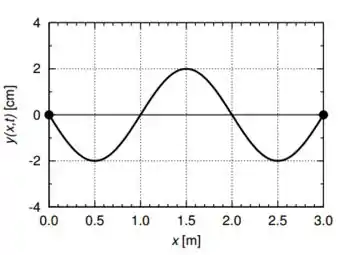
Em um sistema de coordenadas, uma corda homogênea de massa e extremidades fixas em e vibra em seu terceiro harmônico com amplitude máxima de acordo com:
Com dados em metros e em segundos. A figura ao lado mostra a configuração da corda no instante , com o eixo em metros e o eixo em centímetros. Após , observa-se que a corda passa instantaneamente pela primeira vez na configuração de equilíbrio, ou seja, para todo
- Obtenha a velocidade de propagação de ondas na corda.
- Obtenha a tensão na corda.
- Obtenha a forma explícita de considerando e como funções co-seno.
- Calcule as amplitudes e as constantes de fase ( das ondas progressivas e regressiva que, somadas, resultam na onda estacionária acima.
Dica: escreva , e , onde estão associadas as partes espacial e temporal de respectivamente.
Questão 85
Um grupo de pesquisa marinha está desenvolvendo boias com sensores de movimento para monitoração remota de ondas em alto-mar. De forma a testar o equipamento, três dessas boias são posicionadas ao longo de um rio num trecho sem curvas, na proximidade de uma barragem. A boia 1 estava posicionada junto à parede da barragem, a boia 2 está a 16 metros e a boia 3 a 36 metros .Considera as ondas na superfície da água como transversais.
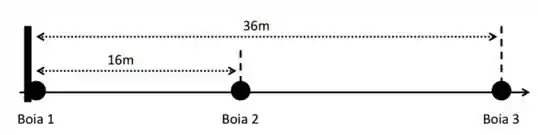
- Se o sensor da boia 2 registrou o movimento após o sensor da boia , qual a velocidade da onda?
- Os sensores registram um movimento oscilatório de período e amplitude .Qual o comprimento de onda e a frequência desta onda.
- Diferentemente dos sensores das boias 2 e 3, o sensor da boia 1 registra que a amplitude de oscilação é de . Escreva a equação da onda incidente, da onda refletida pela barragem, e da onda total resultante ( para definir a fase inicial, assuma que é um ponto de máximo.
- Considerando a interferência entre a onda incidente e a onda refletida, qual será a amplitude de oscilação registrada pelos sensores das boias 2 e 3 após a reflexão?
Questão 86
Duas cordas A e B (ver figura) possuem o mesmo comprimento e a mesma densidade linear, mas a corda A está submetida a uma tensão menor que a corda B. A Figura mostra quatro situações, de (A) a (D), nas quais existem ondas estacionárias nas duas cordas. Em que situação existe a possibilidade de que as cordas A e B estejam oscilando com a mesma freqüência natural?
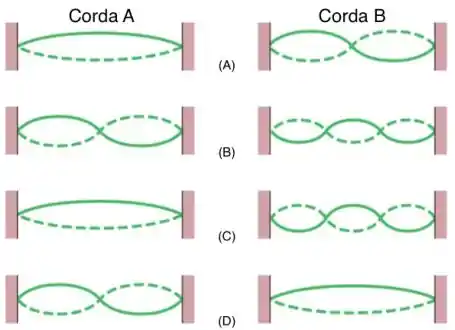
(a) Situação B.
(b) Situação D.
(c) Situação A.
(d) Em nenhuma das situações.
(e) Situação C.
Ver solução completaQuestão 87
Uma corda tem densidade linear de massa e está submetida a uma tração . Para aumentarmos o comprimento das ondas periódicas nesta corda sem modificar o período, a ação correta é:
- Aumentar a amplitude da onda.
- Aumentar .
- Aumentar
- Aumentar o número de onda.
- Aumentar a frequência.
Questão 88
A figura mostra fotografias de diferentes modos de vibração de uma corda de de comprimento e densidade linear , presa por ambas as extremidades e submetida a uma tensão de . As frequências de oscilação transversal da corda para os três casos são
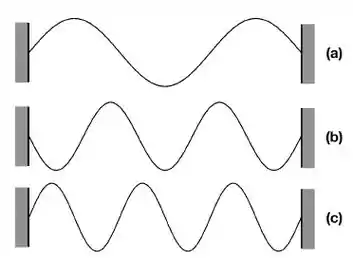
Questão 89
A figura representa uma onda estacionária que oscila em uma corda com frequência . Quantos antinodos (ventres) haverá se a frequência for dobrada para ?

Ver solução completa
Questão 90
Uma corda de violino com de comprimento é colocada próxima a uma fonte sonora que emite um som com frequência de A corda passa então a vibrar no seu segundo modo normal de vibração. Suponha que a corda em repouso coincida com o eixo O-x e que o amortecimento da corda produzido pelo seu atrito com ar possa desprezado.
- Qual a frequência da onda estacionária induzida na corda? Justifique.
- Determine o comprimento de onda na corda.
- Determine a velocidade uma onda nessa corda.
- Determine a posição dos ventres da onda na corda em relação à extremidade
- Sabendo que o movimento de um ponto da corda na posição é dado por ( em , obtenha a função que descreve a onda estacionária na corda.
Questão 91
10 - Uma onda transversal tem suas oscilações no eixo e se propaga ao longo do eixo . A diferença entre um ponto de mínimo e um de máximo da onda no eixo é de e no eixo é de . Suponha que as condições iniciais da mesma resulte em uma constante de fase igual a zero e que a fonte gere as oscilações propagantes em uma taxa de repetições por segundo. Qual a função que melhor descreve esta onda? (Considere em metros e em segundos)
Questão 92
Considere uma corda feita de um material homogêneo. Qual das afirmativas a seguir está INCORRETA?
- Uma onda refletida em uma extremidade tem sempre uma frequência idêntica à onda incidente.
- A soma de uma onda totalmente refletida por uma extremidade e da onda incidente formará sempre uma onda estacionária
- Duas condições de contorno são suficientes para que o número de onda seja quantificado.
- Não há propagação de energia ou de momento numa onda estacionária.
- Uma quantificação do numero de onda não implica numa quantificação da frequência angular.
Questão 93
Uma corda de violino de 30 cm de comprimento com uma massa específica linear de 0,65 g/m é colocada perto de um alto-falante alimentado por um oscilador de áudio de frequência variável. Observa-se que a corda entra em oscilação apenas nas frequências de 880 Hz e 1320 Hz, quando a frequência do oscilador de áudio varia no intervalo de 500 a 1500 Hz.
a) Determine a que harmônicos correspondem as frequências de 880 e 1320 Hz e faça um esboço da forma de oscilação da corda nesses dois modos.
b) Determine a tensão na corda.
Ver solução completaQuestão 94
Uma corda de violino com de comprimento oscila no modo e a velocidade da onda na corda é . Determine o comprimento de onda da onda sonora produzida.
Ver solução completaQuestão 95
A corda de um violino (as duas bordas são fixas) foi afinada de modo que seu primeiro modo normal seja uma onda estacionária de frequência de . A corda possui massa específica linear de e está sujeita a uma tração de . A figura serve como guia.
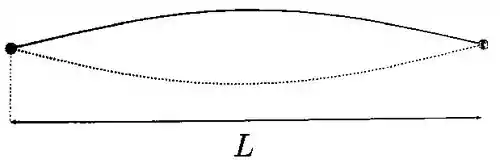
a) Quanto vale o tamanho da corda?
Para que a mesma corda vibre em outra frequência , o violinista a prende com seu dedo em um ponto para que ela vibre em apenas uma fração de tamanho da corda (ver figura) .
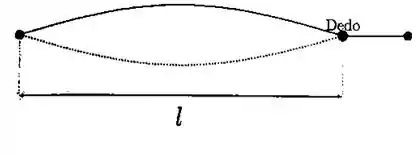
(b) Calcule a razão
Ver solução completaQuestão 96
Duas ondas se propagam em uma mesma corda horizontal muito comprida. Uma das ondas, que se propaga para a esquerda no sentido , é dada por
e a outra onda, que se propaga para a direita no sentido , é dada por
onde e estão dados em metros e em segundos. A superposição das ondas cria uma onda estacionária. Seja a posição do primeiro ventre da corda tal que . A posição no instante é:
a) .
b) .
c) .
d) .
e) .
f) .
g) nenhuma das respostas indicadas.
Ver solução completaQuestão 97
A taxa de transferência de energia por uma onda ao longo de uma corda (a potência instantânea) é dada por:
Onde é a tensão.
- Usando a expressão (1), obtenha para uma onda estacionária dada por:
- Calcule a potência média por período transportada pela onda para todo o
- Para uma onda estacionária dada pela expressão (2), faça gráficos de e do deslocamento em função de para: , , , e .
- Qual o valor da potência instantânea nos nós e nos ventres da onda?
Questão 98
Microondas são enviadas, através de um pequeno orifício, para o interior de uma "cavidade ressonante", a qual consiste de um cilindro de de comprimento com extremidades refletivas (fig). A fonte de microondas pode emitir ondas em
toda a faixa de frequências indo de a . Queremos usar esta fonte para gerar ondas estacionárias com um nó no centro da cavidade. Sendo o índice que enumera os modos normais, isto será possível
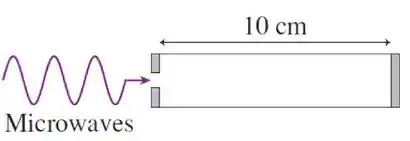
A) para todos os valores ímpares de
B) para todos os valores pares de
C) para certos valores pares de
D) para certos valores ímpares de
E) para nenhum valor de
Ver solução completa