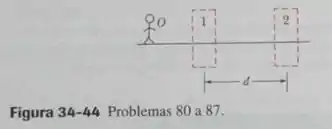
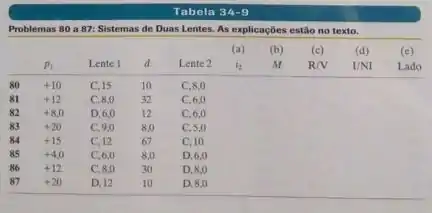
Na Fig 34-44, o boneco (o objeto) está sobre o eixo central comum de duas lentes delgadas simétricas, que estão nas regiões indicadas por retângulos tracejados. A lente 1 está na região mais próxima de , a uma distância do objeto. A lente 2 está na região mais afastada de , a uma distância da lente 1. Para cada problema, a Tabela 34-9 mostra uma combinação diferente de lentes e a diferentes valores das distancias, que são dadas em centímetros. O tipo de lente é indicado por para uma lente convergente e para uma lente divergente; o número que se segue a ou é a distância entre a lente e um dos pontos focais (o sinal apropriado para a distância focal não está indicado).

Determina a distância da imagem produzida pela lente 2 (a imagem final produzida pelo sistema) e a ampliação lateral total do sistema, incluindo o sinal. Determine também se a imagem final é real ou virtual , se é invertida ou não invertida e se está do mesmo lado que a lente ou está do lado oposto .

Fizemos isso para podermos usar a distância da imagem da lente 1 para encontrarmos a distância do objeto da lente 2, já que o objeto dela é a imagem da primeira lente. Então relacionamos a distância entre as lentes com para encontrar :

Usando na equação de lentes delgadas:

Para encontrar :

Lembrando que é negativo, ficamos com:

(b) Agora usamos a equação de ampliação total:

Com os valores que achamos:

Que dá:

(c) Como é negativo, a imagem é virtual .

(d) E como a ampliação total é positiva, a imagem não esta invertida .

(e) E por ser virtual, a imagem se forma do mesmo lado que a lente 2 .