Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 22
Demonstre que a distância focal de uma lente delgada biconvexa pode ser expressa em função do diâmetro da lente, de sua espessura e do seu índice de refração relativo ao meio.
Passo 1
Bom, sabemos que o foco de uma lente delgada é dado por
Nesse expressão, e são os raios de curvatura das superfícies esféricas que dão origem a lente.
Aqui estamos trabalhando com uma lente biconvexa, que é representada a seguir:
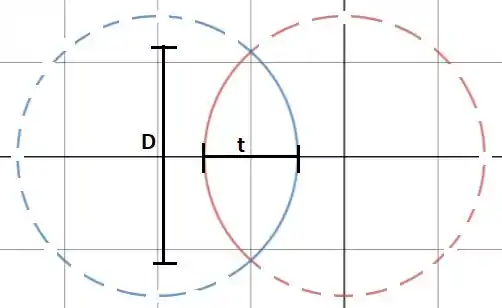
Nesse caso, temos que (esfera vermelha) e (esfera azul). O sinal do raio de curvatura da esfera azul é negativo pois a orientação dela é contrária a da esfera vermelha. Com isso,
Portanto,
Passo 2
Agora vamos usar um pouquinho de geometria analítica. A equação do círculo vermelho é
Note que quando , temos que . Substituindo isso na equação:
Portanto,
Ou ainda,
Aqui vem o pulo do gato: supondo que a espessura é muit pequena, o termo pode ser desprezado em comparação com os demais. Assim,
Passo 3
Substituindo na expressão do foco:
Assim,