Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 25.Exercícios e Problemas - Ex. 39
Uma chapa plana, de espessura , tem uma densidade volumétrica de carga constante . Determine o módulo do campo elétrico em todos os pontos do espaço, tanto (a) dentro como (b) fora da chapa, em termos de , a distância medida a partir do plano central da chapa.
Passo 1
Fala galera, bora lá!
Suponha que a carga total esteja uniformemente distribuída ao longo da chapa. Considerando uma área muito grande, podemos imaginar que o campo elétrico possua uma direção ortogonal ao plano da superfície externa da placa.
A simetria desta chapa uniformemente carregada indica que o módulo do campo varia com a distância . No centro da chapa, a simetria do problema indica que o campo elétrico deve ser nulo, ou seja,
para
Na figura abaixo mostramos uma superfície gaussiana cilíndrica, sendo que a base está alinhada com o plano mediano da chapa.
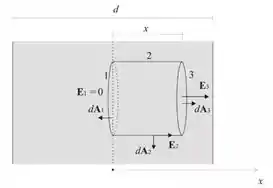
Portanto, concluímos que o fluxo total através da superfície gaussiana cilíndrica é dado por
onde é o módulo do campo elétrico a uma distância do plano central .
Passo 2
(a) A carga englobada no interior da superfície gaussiana cilíndrica é dada pela integral de no volume situado no interior da superfície. Como a densidade de carga é constante, a carga total no interior da superfície é dada por
Sabendo que o campo elétrico é a somatória das cargas dividida pela permissividade elétrica do vácuo
Podemos aplicar a lei de Gauss para a superfície considerada, encontramos facilmente a seguinte resposta:
Passo 3
(b) De maneira semelhante, construímos uma superfície semelhante, onde, agora, a área da base está situada a uma distancia do plano central .
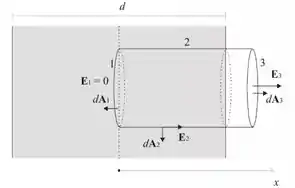
De acordo com a figura, vemos facilmente que temos:
Assim, aplicando a lei de Gauss para a superfície considerada, encontramos a seguinte resposta: