Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 9
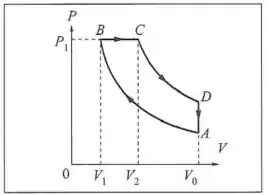
O ciclo Diesel, representado na Fig. P.5, onde e são adiabáticas, esquematiza o que ocorre num motor Diesel de tempos. A diferença em relação ao ciclo de Otto (problema 8) é que a taxa de compressão adiabática é maior, aquecendo mais o ar e permitindo que ele inflame o combustível injetado sem necessidade de uma centelha de ignição: isto ocorre a pressão constante, durante o trecho ; a taxa de expansão adiabática associada a é . (a) Mostre que o rendimento do ciclo Diesel é dado por
(b) Calcule para , , . (c) Compare o resultado com o rendimento de um ciclo de Carnot entre as mesmas temperaturas extremas.
Passo 1
(a) Já que as curvas e são adiabáticas, o único trecho em que o calor é absorvido é .
O trecho também tem troca de calor, mas como a temperatura está diminuindo, o calor não está sendo absorvido pelo gás.
Vamos calcular esse calor usando a primeira lei da termodinâmica:
E agora é só reescrever o primeiro termo usando a lei dos gases ideais:
E o segundo termo usando
Passo 2
Ok, agora vamos calcular o trabalho realizado nos trechos e , usando a fórmula para o trabalho realizado em um trecho adiabático:
E o resultado vai ser o mesmo no outro trecho:
Agora já temos tudo para calcular o rendimento:
Ok, ficou bem confuso, vamos tentar simplificar.
Primeiro dividimos tudo por e multiplicamos tudo por :
Agora dá pra cancelar algumas coisas no numerador:
Passo 3
E como demonstrar a outra parte da igualdade? Temos que usar essa fórmula aqui para os processos adiabáticos:
No trecho :
Olhando pro gráfico, dá pra reescrever esses volumes:
Mas e , então:
E voltando na fórmula do rendimento:
Passo 4
Fica difícil simplificar essa última fórmula sem saber alguma relação entre e .
Vamos usar a lei dos gases ideais pra resolver esse problema:
Usando e :
Substituindo isso na fórmula de antes:
E aí dá pra cortar o :
Multiplicando em cima e embaixo por :
E pra deixar na mesma forma do enunciado é só perceber que:
Então:
Pronto, demonstramos!
Passo 5
(b) Agora é só substituir os valore numéricos para calcular :
Como , e :
Passo 6
(b) Se você colocasse um ciclo de Carnot pra operar entre essas duas temperaturas, o rendimento dele seria o seguinte:
Já que e são as duas temperaturas extremas.
Lá atrás, nós encontramos essas duas relações para as temperaturas:
Ou seja:
Então:
E então, usando os mesmos valores de antes, o rendimento do ciclo de Carnot é:
Resposta
(a) Demonstração.
(b) .
(c) O rendimento do ciclo de Carnot seria .