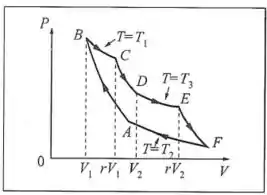
O ciclo da Fig. P.7. é formado por isotermas de temperaturas (BC), () e (FA), e pelas adiabáticas , e . As taxas de expansão isotérmicas e , são ambas iguais a . Calcule o rendimento do ciclo e mostre que é menor do que o rendimento de um ciclo de Carnot entre as mesmas temperatuas extremas:

Todos esses três trechos são isotérmicos. Então, pela primeira lei da termodinâmica:

E então é só usar a fórmula do trabalho no caminho isotérmico:

Já que .

E o calor no processo também seria bem simples:

O problema é que a gente ainda não sabe a razão entre os volumes e . E é isso que nós vamos descobrir agora.

Nos trechos adiabáticos, , e , dá pra aplicar essa fórmula aqui:

Vamos aplicar isso nos três trechos adiabáticos pra fazer um sistema de três equações:

Se você der uma olhada no gráfico, já consegue achar algumas variáveis pra substituir nesse sistema:

E a ideia é resolver esse sistema pra encontrar .

Dividindo a primeira equação pela segunda:

E pela terceira equação, dá pra escrever o seguinte:

Substituindo isso na expressão de antes:

Elevando os dois lados a :

Beleza, conseguimos a razão que a gente queria. Agora dá pra calcular o calor no processo :

Agora vamos voltar na fórmula lá do passo :

E substituir tudo que já calculamos:

E dá pra cortar bastante coisa nessa fração:

Pronto, chegamos na fórmula para o rendimento.

Se tivéssemos um ciclo de Carnot operando entre as temperaturas extremas, o rendimento seria:

E o que nós calculamos é:

Ou seja, trocamos pela média das temperaturas e no denominador:

E quanto maior for o termo no denominador, menor é a fração e maior é o rendimento.

Ou seja: