Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 78

Um cilindro comprido, com seu eixo orientado ao longo do eixo O z , possui uma densidade de corrente J → . A densidade de corrente, embora seja simétrica em relação ao eixo do cilindro, não é constante e varia de acordo com a relação

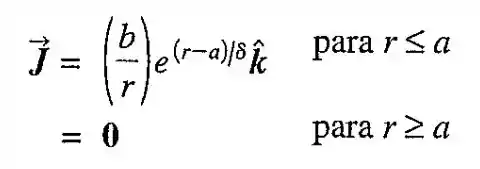
Em que o raio de cilindro é a = 5.0   c m , r é a distância radial entre o ponto considerado e o eixo do cilindro, b é uma constante igual a 600   A / m e δ é uma constante igual a 2.50 c m .

( a ) Suponha que I 0 em termos de b , δ e a . Avalie sua expressão para obter um valor numérico para I 0 .

( b ) Usando a lei de Ampére, deduza uma expressão para o módulo do campo magnético B → na região r ≥ a . Expressa sua resposta em termos de I 0 em vez de b .

( c ) Obtenha uma expressão para a corrente I contida em uma seção reta circular de raio r ≤ a e centralizada sobre o eixo do cilindro. Expresse sua resposta em termos de I 0 em vez de b .

( d ) Aplicando a lei de Ampére, deduza uma expressão para o módulo do campo magnético B → na região r ≤ a

( e ) Avalie o campo magnético em r = δ ,   r = a e r = 2 a

Passo 1

Para achar a corrente basta fazer:

I 0 = ∫ J → ⋅ d A →

Onde o elemento de área será em coordenadas polares ou seja d A = r d r d θ (pois é a área de um círculo de raio r na forma polar), logo:

I 0 = ∫ b r e r - a δ ⋅ r d r d θ

Em que r vai de 0 até a (onde a é o raio) e θ de 0 até 2 π , então:

I 0 = 2 π b ∫ 0 a e r - a δ d r

Separando e r - a δ , nós teremos:

I 0 = 2 π b e - a δ ∫ 0 a e r δ d r

I 0 = 2 π b e - a δ δ e r δ 0 a  

Aplicando o intervalo:

I 0 = 2 π b δ e - a δ   e a δ - 1 = 2 π b δ 1 - e - a δ

Como a = 5.0   c m , b = 600 A m , δ = 2.5   c m , logo I 0 será:

I 0 = 2 π ⋅ 600 ⋅ 2.5 × 10 - 2 1 - e - 5 × 10 - 2 2.5 × 10 - 2 = 81.49   A

Passo 2

Pela lei de ampere nós teremos que o campo magnético na letra b será de:

B ⋅ 2 π r = μ 0 I

B = μ 0 I 2 π r

Pois consideraremos uma linha igual a circunferência de raio r que está distante do centro da área do cilindro.

Passo 3

Para a letra c nós devemos fazer a mesma integral feita na letra a :

I r = ∫ b r e r - a δ ⋅ r d r d θ

Só que r vai de 0 até um valor qualquer r e θ continua de 0 até 2 π nos dando:

I r = 2 π b e - a δ ∫ 0 r e r δ d r

I r = 2 π b δ e - a δ e r δ 0 r

I r = 2 π b δ e -   a δ e r δ - 1

I r = 2 π b δ e r - a δ - e - a δ

Dividindo por I 0 nós teremos:

I r I 0 = 2 π b δ e r - a δ - e - a δ 2 π b δ 1 - e - a δ

I r = I 0 e -   a δ e r δ - 1 1 - e - a δ

Dividindo em cima e embaixo por e - a δ nós temos:

I r = I 0 e r δ - 1 e   a δ - 1

Passo 4

Agora o campo magnético para uma distância radial menor que o raio do cilindro será:

B ⋅ 2 π r = μ 0 I r

Pois agora o raio da circunferência será uma distância r < a e a corrente será proporcional a densidade da corrente (não a área, pois a corrente não está uniforme) e que será a I r , logo o campo magnético será de:

B = μ 0 ⋅ I 0 e r δ - 1 e   a δ - 1 2 π r

B = μ 0 I 0 e r δ - 1 2 π r e   a δ - 1

Passo 5

Voltando com a informação que a = 5.0   c m , b = 600 A m , δ = 2.5   c m e I 0 = 81.49   A

Nós teremos que para r = δ :

B r = δ = μ 0 I 0 e δ δ - 1 2 π r e   a δ - 1 = μ 0 I 0 e - 1 2 π δ e a δ - 1 = 4 π × 10 - 7 ⋅ 81.49 e - 1 2 π ⋅ 2.5 × 10 - 2 e 2 - 1 = 1.75 × 10 - 4 T

B r = a = μ 0 I 0 e δ δ - 1 2 π r e   a δ - 1 = μ 0 I 0 e a δ - 1 2 π a e a δ - 1 = 4 π × 10 - 7 ⋅ 81.49 2 π ⋅ 5 × 10 - 2 = 3.26 × 10 - 4 T

B r = 2 a = μ 0 I 0 2 π ( 2 a ) = 4 π × 10 - 7 ⋅ 81.49 4 π ⋅ 5 × 10 - 2 = 1.63 × 10 - 4   T

Como r > a no terceiro caso nós devemos lembrar do comportamento do campo magnético que será de simplesmente B = μ 0 I 2 π r

Resposta

a )   I 0 = 81.49   A

b )   B = μ 0 I 2 π r

c )   I r = I 0 e r δ - 1 e   a δ - 1

d ) B = μ 0 I 0 e r δ - 1 2 π r e   a δ - 1  

e )   B δ = 1.75 × 10 - 4 T

B ( a ) = 3.26 × 10 - 4 T

B 2 a = 1.63 × 10 - 4   T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A espira retangular da figura, de lados a e b , é percorrida por uma corrente i . Calcule a força F → exercida sobre ela por um fio retilíneo longo, que transporta uma corrente i ' , situado à uma dis
Nas figs. (a) e (c), as porções retilíneas dos fios são supostas muito longas e a porção semicircular tem raio R . A corrente tem intensidade i . Calcule o campo B → , em módulo, direção e sentido, no
Duas bobinas circulares coaxiais idênticas, de espessura desprezível, com N espiras de raio a em cada bobina, transportam correntes de mesma intensidade i e mesmo sentido, e estão colocados uma acima
O circuito da figura, formado por sois latos retilíneos e dois arcos de círculo, subtendendo um setor circular de ângulo θ , é percorrido por uma corrente de intensidade i . Calcule o campo magnético
Uma espira em forma de retângulo, de lados 2 a e 2 b , transportam uma corrente de intensidade i .Calcule a magnitude do campo magnético no centro do retângulo.Tome o limite do resultado para a ≫ b e