Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 70

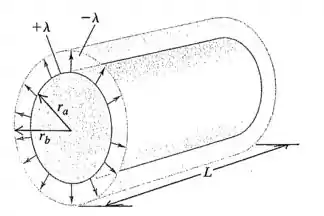
O cilindro interno de um capacitor cilíndrico longo possui um raio r a e uma densidade linear + λ . Ele é circundado por um condutor cilíndrico co-axial com raio interno r b e densidade de carga linear - λ . (a) Qual é a densidade de energia na região entre os condutores a uma distância r do eixo? (b) Integre a densidade de energia calculada na parte (a) sobre o volume entre os condutores em um comprimento L do capacitor, para obter a energia total do campo elétrico por unidade de comprimento. (c) Use a equação U = Q 2 2 C e a capacitância por unidade de comprimento encontrada C = 2 π ϵ o L   l n - 1 r b r a para calcular U / L . O resultado obtido concorda com o resultado que você encontrou no item (b)?

Passo 1

letra a)

A densidade de energia é dada pela expressão:

u = 1 2 ϵ o E 2

Para a região entre os cilindros, o campo elétrico é:

E = λ 2 π ϵ o r

Então a densidade de corrente será:

u = 1 2 ϵ o λ 2 π ϵ o r 2

u = λ 2 8 π 2 ϵ o r 2

Passo 2

letra b)

A energia total será:

U = ∫ r a r b u 2 π L r d r = 2 π L ∫ r a r b λ 2 8 π 2 ϵ o r 2 r d r

U = 2 π L λ 2 8 π 2 ϵ o ∫ r a r b 1 r d r

U = L λ 2 4 π ϵ o l n ( r ) r a r b

U = λ 2 L 4 π ϵ o l n r b r a

Por unidade de comprimento:

U L = λ 2 4 π ϵ o l n r b r a

Passo 3

letra c)

A energia de um capacitor é dada por:

U = Q 2 2 C

E a capacitância o enunciado no deu. Então:

U = Q 2 2 2 π ϵ o L   l n - 1 r b r a

U = Q 2 4 π ϵ o L   l n r b r a

Como a carga pode escrita Q = λ L

U = λ L 2 4 π ϵ o L   l n r b r a

U = L λ 2 4 π ϵ o   l n r b r a

Então: U / L será:

U L = λ 2 4 π ϵ o l n r b r a

Sendo esse resultado igual ao resultado da letra b.

Resposta

letra a) u = λ 2 8 π 2 ϵ o r 2

letra b) U L = λ 2 4 π ϵ o l n r b r a

letra c) U L = λ 2 4 π ϵ o l n r b r a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Determine (a) q 3 ; (b) V 3 ; (c) a energi
Um capacitor de placas paralelas é conectado a uma bateria. O espaço entre as placas está vazio. Se a separação entre as placas é triplicada enquanto o capacitor permanece conectado à betaria, qual é
Se a tensão em um capacitor de placas paralelas é duplicada, sua capacitância (a) dobra, (b) cai à metade, (c) permanece a mesma?
Se o capacitor do problema 5 é desconectado da bateria antes de a separação entre as placas ser triplicada, qual é a razão entre as energias final e inicial armazenadas?
Se a distância entre as placas de um capacitor de placas paralelas, carregado e isolado é duplicada, qual é a razão entre as energias final e inicial armazenadas?