Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 25
Um cilindro, de massa e raio , rola até um degrau de altura , como mostrado na figura. Quando uma força horizontal de magnitude é aplicada no topo do cilindro, este permanece em repouso. (a) Determine uma expressão para a força normal exercida pelo piso sobre o cilindro. (b) Determine uma expressão para a força horizontal exercida pela borda do degrau sobre o cilindro. (c) Determine uma expressão para a componente vertical da força exercida pela borda do degrau sobre o cilindro.
Passo 1
Se liga na situação de quando o cilindro tá coladinho no degrau:
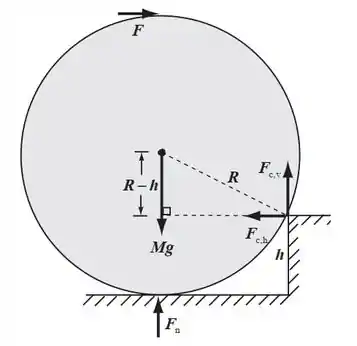
Então como é que é? O cilindro tá em equilíbrio, né? Então vamos fazer equilíbrio dos momentos e das forças horizontais e verticais. Bora lá então!
Passo 2
- Em relação ao ponto de contato com o degrau, o peso faz momento anti-horário, e a normal e a força fazem momento horário. Equacionando isso, vamos ter:
- Fazendo o equilíbrio das forças na horizontal:
- Agora a gente faz equilíbrio das forças na vertical.
Achamos uma expressão para a normal, mas com essa letra estranha que representa a distância horizontal do centro ao ponto de contato. Mas olha só, podemos aplicar Pitágoras naquele triângulo pontilhado!
Substituindo isso na expressão da normal:
Passo 3
Essa foi mole!