Um mastro de sustentação uniforme horizontal com comprimento de m e pesando N está articulado numa parede vertical a uma de suas extremidades. Uma dublê de cinema pesando N está suspensa em sua outra extremidade. O mastro está suportado por um cabo que liga sua extremidade livre a um ponto da parede diretamente acima do contato com o mastro. a) Sabendo que a tensão no cabo não deve exceder N, qual é a altura mínima acima do mastro em que o cabo deve ser ligado à parede? b) Supondo que o cabo está ligado a um ponto da parede situado a m abaixo desse ponto, qual deve ser o aumento da tensão em newtons para que o mastro permaneça na direção horizontal?
Passo 1
Faaala galeraa, bora fazer mais uma questão?
O enunciado pediu pra gente encontrar a altura mínima acima do mastro em que o cabo deve ser ligado a parede, sabendo que a tensão no cabo é de . E encontrar o valor do aumento de tensão necessário para que o mastro permaneça na direção horizontal.
Bora começar fazendo um diagrama de corpo livre pra entender o que tá acontencendo, ok? Aqui vamos representar a direção do cabo que ficará preso na parede na altura .
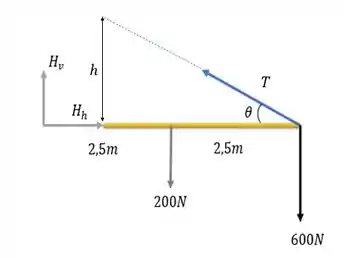
Nossos primeiro objetivo vai ser encontrar a altura do mastro, para isso vamos precisar encontrar o valor das componentes do cabo. Um bom jeito é fazer o somatório dos torques em algum ponto e é isso o que vamos fazer.
Lembrando da condição de equilíbrio:
Vamos lá!
Passo 2
a) Tomando os torques sobre a extremidade articulada do mastro, vamos ter:
E aqui um detalhe é que os esforços que estão em cima do eixo de rotação não causam torque pois sua distância do eixo é nula.
Então, calculando os produtos e isolando a componente de tensão na nossa equação, vamos ter:
Passo 3
Se liga nesse bizu aqui, se o módulo da força tem que ser no máximo de , a gente pode usar o teorema de Pitágoras pra encontrar o valor de por meio do triângulo retângulo formado na nossa figura. Assim, temos:
E para encontrarmos a direção, calculamos a tangente do ângulo usando as relações no triângulo formado, ou seja:
Então, substituindo os valores das componentes da tensão calculadas, temos que a altura acima do poste em que o fio se encontra será:
Passo 4
b) Agora supondo que o cabo está ligado a um ponto da parede situado a m abaixo desse ponto, a componente da tensão permanece , mas a altura cai em . Então, vamos usar a mesma equação da tangente, porém com a nova altura diminuída.
Substituindo temos:
E calculando o ângulo, obtemos:
Então, substituindo na equação:
Teremos:
Logo, houve um aumento de tensão de .
Isso acontece porque à medida que o fio é preso mais próximo da extremidade articulada do poste, o braço do momento para diminui e deve aumentar para produzir o mesmo torque nesse sentido.
Valeu, galera! Até a próxima! 😉
Resposta
- Um aumento de