Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 35

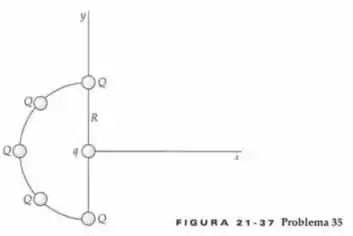
Cinco cargas puntiformes idênticas, cada uma com carga , estão igualmente espaçadas em um semicírculo de raio , como mostra a Figura 21-37. Determine a força (em termos de , e ) em uma carga localizada em um ponto equidistante das cinco outras cargas.

Passo 1

Nesse problema será bom a gente usar um pouquinho de noção de simetria.

Veja que a carga superior e a carga inferior cancelam a força uma da outra, concorda? As cargas nas diagonais devem cancelar o força no eixo y uma da outra, dando uma força resultante no eixo x. A última carga também faz uma força no eixo x. Logo, temos que a força resultante deve estar no eixo x.

Agora, veja a figura a seguir.

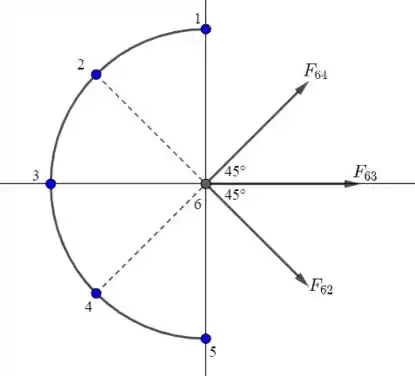
Temos que

A resultante entre e é:

Segue que,

Em notação vetorial, temos

Resposta

A força resultante é

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 21-36 mostra quatro esferas condutoras iguais, que estão separadas por grandes distâncias. A esfera W (que estava inicialmente neutra) é colocada em contato com a esfera A e depois as esferas s

Na Fig. 21-37, a partícula 1 , de carga + 4 e , está a uma distância d 1=2,00m m do solo e a partícula 2 , de carga + 6 e , está sobre o solo, a uma distância horizontal d 2=6,00m m da partícula 1 . Q

Na Fig. 21-38, duas pequenas esferas condutoras de mesma massa m e mesma carga q estão penduradas em fios não condutores de comprimento L . Suponha que o ângulo θ é tão pequeno que a aproximação t a n

Cargas pontuais de + 6,0μ C e -4,0μ C são mantidas fixas no eixo x nos pontos x=8,0m e x=16m , respectivamente. Que carga deve ser colocada no ponto x=24m para que a força eletrostática total sobre um

Na Fig. 21-40, três esferas condutoras iguais são dispostas de modo a formar um triângulo equilátero de lado d=20,0c m . Os raios das esferas são muito menores que d e as cargas das esferas são q A=-2