Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 36

A estrutura molécula N H 3 é aproximadamente a de um tetraedro equilátero, onde três íons H + formam a base e um íon N - 3 está no ápice do tetraedro. O comprimento de cada lado é 1,64 × 10 - 10   m . Calcule a força elétrica exercida em cada íon.

Passo 1

Inicialmente, note que os módulos das forças são simples de se calcular. Já que todas estão a uma mesma distância uma da outra, segue que

F = k q 1 q 2 a 2

Note que a carga do íon N - 3 é - 3 e e a carga do H + é + e . Sendo assim, temos que

F = 9 × 10 9 λ ⋅ 1,6 × 10 - 19 1,6 × 10 - 19 1,64 × 10 - 10 2 = 8,56 × 10 - 9 λ     N

onde λ = - 3 se estivermos calculando a força entre H + e N - 3 e λ = 1 se estivemos calculando a força entre H + e H + .

Passo 2

O que é mais complicado é determinarmos a direção dessas forças. Para tal, podemos nos valer das coordenadas. Podemos pensar que a base do tetraedro é:

R 1 = - a 2 , 0,0 R 2 = a 2 , 0,0 R 3 = 0 , 3 2 a , 0 R 4 = 0 , 3 6 a , 6 3 a

Cada um desses vértices será a posição de uma carga, sendo o vértice R 4 ocupado pelo N - 3 . Veja:

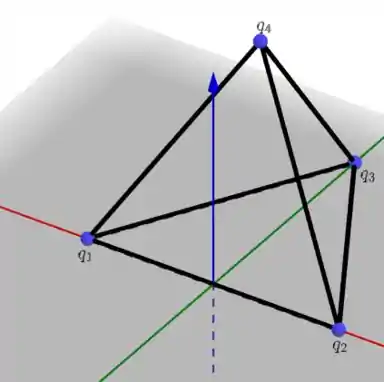
Passo 3

Por simetria, as forças exercidas em cada íon H + são iguais. Portanto, vamos calcular apenas uma dessas forças. Para isso, vamos calcular os vetores posição relativa de cada carga.

  • Entre 1 e 2 :

    • r ^ 12 = R → 1 - R → 2 R → 1 - R → 2 = - a ,   0,0 - a , 0,0 = - 1,0 , 0

  • Entre 1 e 3 :

    • r ^ 13 = R → 1 - R → 3 R → 1 - R → 3 = - a 2 , - 3 2 a , 0 - a 2 , 3 2 a ,   0 = - 1 2 , - 3 2 , 0

  • Entre 1 e 4 :

r ^ 14 = R → 1 - R → 4 R → 1 - R → 4 = - a 2 , - 3 6 a , - 6 3 a - a 2 ,   - 3 6 a ,   - 6 3 a = - 1 2 , - 3 6 , - 6 3

Portanto, temos que a força em 1 é:

F → 1 = 8,56 × 10 - 9 r ^ 12 + r ^ 13 - 3 r ^ 14 F → 1 = 8,56 × 10 - 9 0 ,   0 , 6 F → 1 = 8,56 × 10 - 9 6   k ^ = 2,10 × 10 - 8 N   k ^

Passo 4

Assim, F → 2 = F → 3 = F → 1 = 2,10 × 10 - 8   N   k ^ . A condição de equilíbrio da molécula é que:

F → 1 + F → 2 + F → 3 + F → 4 = 0 ∴ F → 4 = - 3 F → 1 F → 4 = - 6,30 × 10 8   N   k ^

Resposta

No H + : 6,30 × 10 8   N ; No N 3 - : 2,10 × 10 - 8   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O modelo de Bohr para o átomo de hidrogênio pode ser comparado ao sistema Terra-Lua, em que o papel da Terra é desempenhado pelo próton e o da Lua pelo elétron, a atração gravitacional sendo substituí
Em um litro de hidrogênio gasoso, nas condições NTP: a) Qual é a carga positiva total contida nas moléculas e neutralizada pelos elétrons? b) Suponha que toda a carga positiva pudesse ser separada da
Uma carga negativa fica em equilíbrio quando colocada no ponto médio do segmento de retaque une duas cargas positivas idênticas. Mostre que essa posição de equilíbrio é estável parapequenos deslocamen
Cargas q, 2q e 3q são colocadas nos vértices de um triângulo equilátero de lado a. Uma carga Q de mesmo sinal que as outras três é colocada no centro do triângulo. Obtenha a força resultante sobre Q (
Duas esferinhas idênticas de massa m estão carregadas com carga q e suspensas por fios isolantes de comprimento l. O ângulo de abertura resultante é 2 θ . Mostre que q 2 c o s θ = 16πϵ 0 l 2m gs e n 3