Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 39
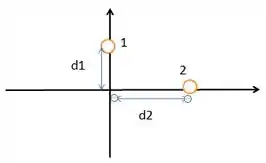
Na Fig. 21-38, a partícula de carga , está a uma distância do solo e a partícula , de carga , está sobre o solo, a uma distância horizontal da partícula . Qual é a componente da força eletrostática exercida pela partícula
sobre a partícula ?
Passo 1
Fala aí! tudo certinho? 😬
Nesse problema temos duas partículas onde e . A partícula está a do solo e está a uma distância horizontal de .
A partir daí queremos obter a componente da força eletrostática que a partícula faz sobre a partícula .
Tem ideia de como fazemos isso? 🤔
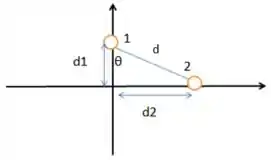
Aqui, basta aplicarmos a fórmula da força eletrostática. Para encontrarmos a componente , basta fazermos a projeção dessa força sobre esse eixo.
Como a fórmula da força eletrostática é:
Onde: é a força eletrostática; é a constante eletrostática e vale ; é a carga da partícula 1 e vale ; é a carga da partícula 2 e vale e é a distância entre as duas partículas.
Veja só! 😁
Passo 2
Assim, a primeira coisa que precisamos fazer é determinar essa distância . Por formar um triângulo retângulo, encontramos a hipotenusa do triângulo em função de seus catetos e :
Vamos aplicar essa definição então na fórmula da força eletrostática:
Agora temos uma equação que sabemos todas os valores do enunciado:
Tranquilo até aqui? 😉
Passo 3
Vamos substituir os valores que identificamos no último passo? Assim, olha:
Lembrando que passamos as distâncias e para suas medidas em metros!
Agora que unidade é essa ? Deixa que eu te explico, nada mais é que a unidade de carga de um próton e vale:
Então vamos substituir esse valor na nossa equação também:
Fazendo então essa conta vamos achar o seguinte:
Mas nós queremos não a força total e sim a componente !
Bacana, não é? 😎
Passo 4
Tudo bem é só a gente decompor essa força. Você concorda comigo que a decomposição em e é proporcional às distâncias? Olha aqui melhor:
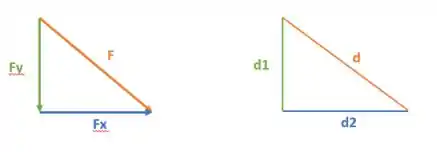
Logo podemos fazer:
Como queremos descobrir :
Substuindo os valores que encontramos:
E api! Entendeu tudo? Responde Aí! 😬
