Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.10 - Ex. 59
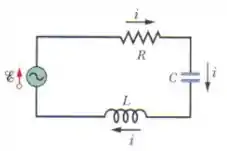
Em um circuito como o da Fig. 31-7, suponha que , , e . (a) Para que valor de capacitância a potência dissipada na resistência é máxima? (b) Para que valor de capacitância a potência dissipada na resistência é mínima? Determine (c) a dissipação máxima; (d) o ângulo de fase correspondente; (e) e o fator de potência correspondente. Determine também (f) a dissipação mínima; (g) o ângulo de fase correspondente; (h) o fator de potência correspondente.
Passo 1
Fala aí! 😉
O problema fala sobre um circuito e pede para fazermos considerações quanto a potência dissipada na resistência.
A potência dissipada na resistência é dada por:
Porém,
Assim,
Essa é a potência instantânea. Lembrando que e usando que o valor médio do seno ao longo de um período é , obtemos que a potência média dissipada é
Como , temos que
Veja só! 😁
Passo 2
A potência dissipada é máxima quando o denominador for mínimo. Isso ocorre para . Assim,
Substituindo e , obtemos
Neste caso, a potência é dada por
Como , fase será nula:
Logo,
O fator de fase da potência será
Tranquilo até aqui? 😁
Passo 3
No item (b) queremos que a potência seja mínima e para isso, deve ser máximo. Note que se , , de modo que essa é a situação em que a potência é mínima. Neste caso, como , a potência dissipada é nula.
Como , temos que
Assim,
Portanto, o fator de fase será
E aí! o que achou? Responde Aí! 😊
